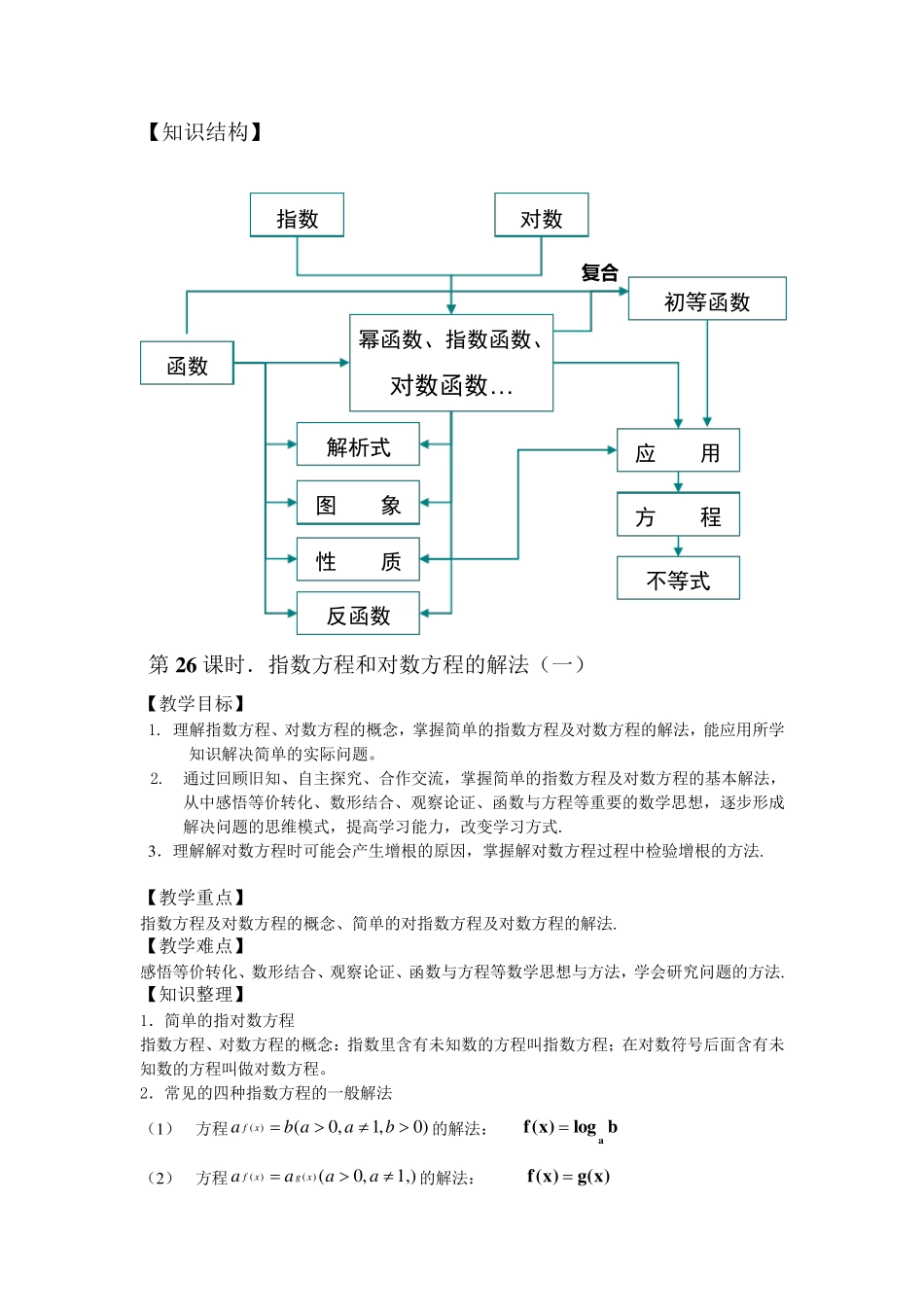
第三章 幂函数、指数函数和对数函数 【教材解读】 幂函数是中学教材中的一个基本内容,即是对正比例函数、反比例函数、二次函数的系统总结,也是对这些函数的概况和一般化. 指数函数是中学教材中的一个基本内容,是最重要的初等函数之一;它在反函数概念及对数函数概念的引入和学习中起关键作用;对培养学生的数学能力、特别是形成正确的数学观念有非常积极的作用. 为了解决“已知底数和幂的值,求指数的问题”,引入了对数。对数这一内容本身就是学生第一次学习,因而掌握对数的运算非常重要.一方面,对数的运算要为后面学习对数函数以及对数方程起到铺垫的作用;另一方面,对数的运算和实数的运算有很大的区别.这一部分里证明性质时强调了与指数运算的结合,为后面讲解反函数作铺垫.当然在这个内容中运算法则的熟练运用尤为重要。 为了解决不同底数的对数式之间的运算,引入了换底公式. “反函数”是《高中代数》第一册的重要内容.这一节课与函数的基本概念有着紧密的联系,通过对这一节课的学习,既可以让学生接受、理解反函数的概念并学会 反函数的求法,又 可使 学生加 深 对函数基本概念的理解,还 为今 后反三角 函数的教学做 好 准 备 ,起到承 上 启下 的重要作用. “对数函数的图 像 与性质”是继 学生学习了指数函数的图 像 与性质、对数概念及其 运算、反函数的概念等知识 之后的一节重要内容,是基本初等函数研 究 的继 续 ,是数形结合的典 型课例;它是解指数方程、对数方程及其 不等式的基础 ,是解决一些物 理、化学、经 济 学等实际 问题的重要工 具 ,更 是高考 的热 点 之一. 在本节课的学习中,涉 及到数形结合、类 比归 纳 、分类 讨 论 等数学思 想 ,对培养学生的辨 证思 维 能力,培养学生的创 新 意 识 有很大的帮 助 . 是幂函数、指数函数等基本初等函数研 究 的继 续 ;它是解指数方程、对数方程及其 不等式的基础 . 在本节课的学习中,涉 及到整 体 代换、数形结合、分类 讨 论 等数学思 想 ,对培养学生的综 合思 维 能力,提 高学生的思 辩 能力有很大的帮 助 . 指数方程是一种 超 越 方程,以学生目 前 的知识 只 能解决一些常规 类 型 的并且 是简 单 的指数方程.因此 这部分内容的学习,一是要求学生掌握简 单 的指数方程的解法,主 要有换元 法和取 对数法,将 指数方程转 化为代数方程...