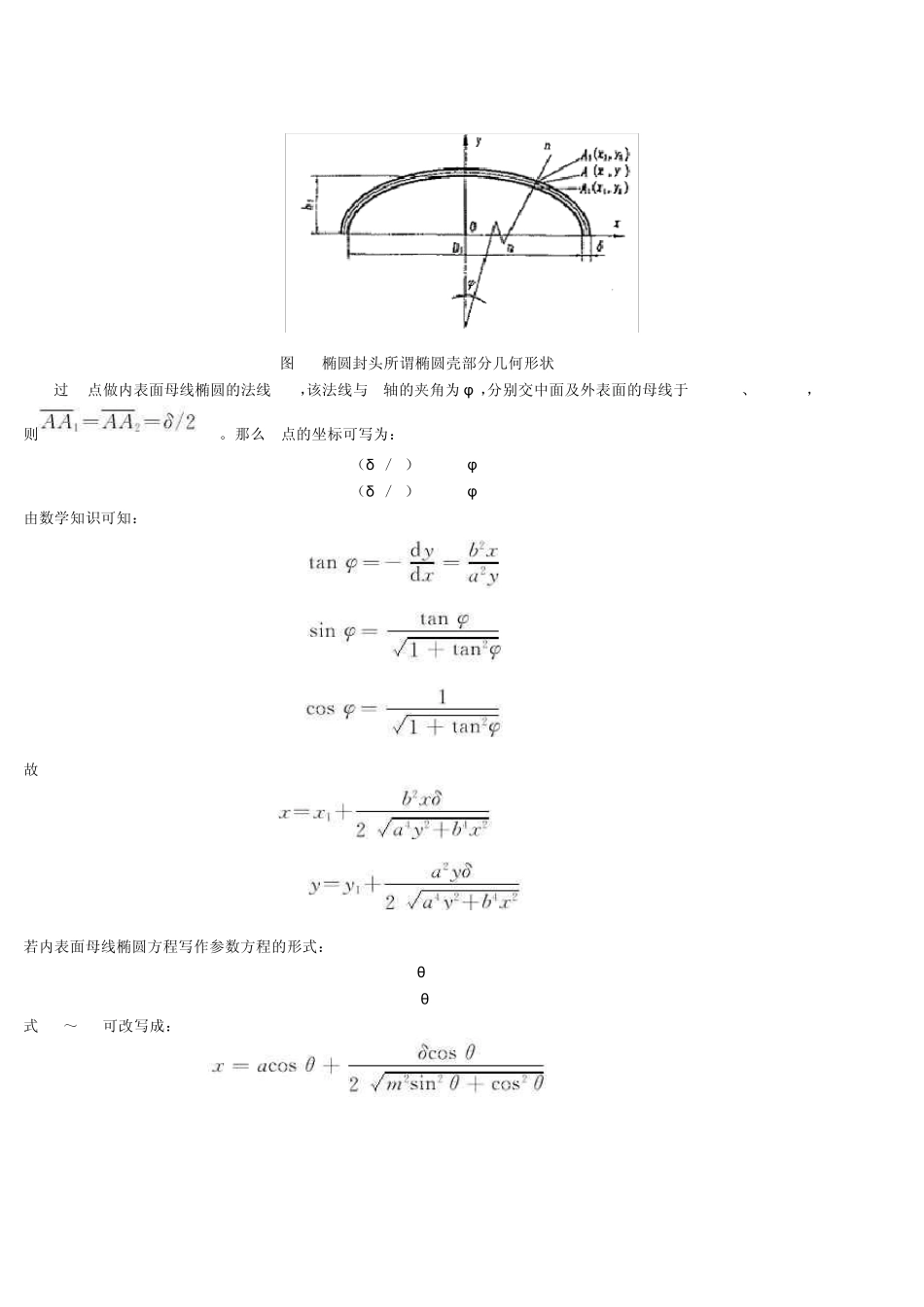
椭圆封头几何形状讨论及展开面积计算 符号说明 a,am——椭圆的长半轴,mm b,bm——椭圆的短半轴,mm Di,Do——椭圆封头的内外径,mm Dm——封头的中径,mm h——封头的直边高度,mm hi——椭圆封头的曲面深度,mm ho——椭圆封头的曲面高度,mm m——椭圆的长短轴之比,m=a/b α ——封头的厚径比,α =δ /Di δ ——封头的厚度,mm 椭圆封头由于受力较好,加工较易,因此被广泛应用于化工、轻工、石油及制药等行业的中低压容器。人们通常认为椭圆封头是由半个椭圆壳和一段直边圆筒组成的,椭圆封头制造时封头展开面积就是根据这一假设推导计算的,然而构成椭圆封头的那半个椭圆壳是不是真正的椭圆壳呢?如果不是,又当如何计算椭圆封头的展开面积呢?笔者根据回转壳体的基本概念详细分析椭圆封头的几何形状,并根据椭圆封头真正的几何形状推导其展开面积,为制造提供准确的下料尺寸。 1 椭圆封头几何形状 1.1 回转壳体基本概念 壳体是被两个曲面所限定的物体,等分壳体各点厚度的曲面称为壳体的中面,中面是回转曲面的壳体称为回转壳体,而回转曲面则是一条平面曲线绕同平面的一根轴旋转而成的曲面,并称这条平面曲线为该回转曲面的母线。回转壳体尤其是回转薄壳的几何形状通常根据中面母线来描述。 1.2 中面母线方程 等厚度的椭圆封头无疑也是一个回转壳体,但无论是冲压还是旋压成型的椭圆封头只能保证其椭圆壳部分的内表面(或外表面)为椭球面,中面及外表面(或内表面)并非椭球面,即其内表面(或外表面)母线是椭圆,而中面及外表面(或内表面)母线并非椭圆。中面及外表面(或内表面)母线方程可以根据内表面(或外表面)母线椭圆按如下方法推出。 假定椭圆封头椭圆壳部分的内表面母线是椭圆,见图 1。已知内表面母线上一点 A1(x1,y1),其坐标应满足椭圆方程: (1) 式中,a=Di/2, b=hi。 图1 椭圆封头所谓椭圆壳部分几何形状 过A1点做内表面母线椭圆的法线n-n,该法线与y轴的夹角为φ ,分别交中面及外表面的母线于A(x,y)、A2(x2,y2),则。那么 A点的坐标可写为: x=x1+(δ /2) sin φ (2) y=y1+(δ /2) cos φ (3) 由数学知识可知: 故 (4) (5) 若内表面母线椭圆方程写作参数方程的形式: x1=acosθ (6) y1=bsin θ (7) 式(4)~(5)可改写成: (8) (9) 式(8)~(9)即为椭圆封头所谓椭圆壳部分的中面母线参数方程,同理可写出其外表面母线的参数方程,在此不再赘述。 根据回转壳体...