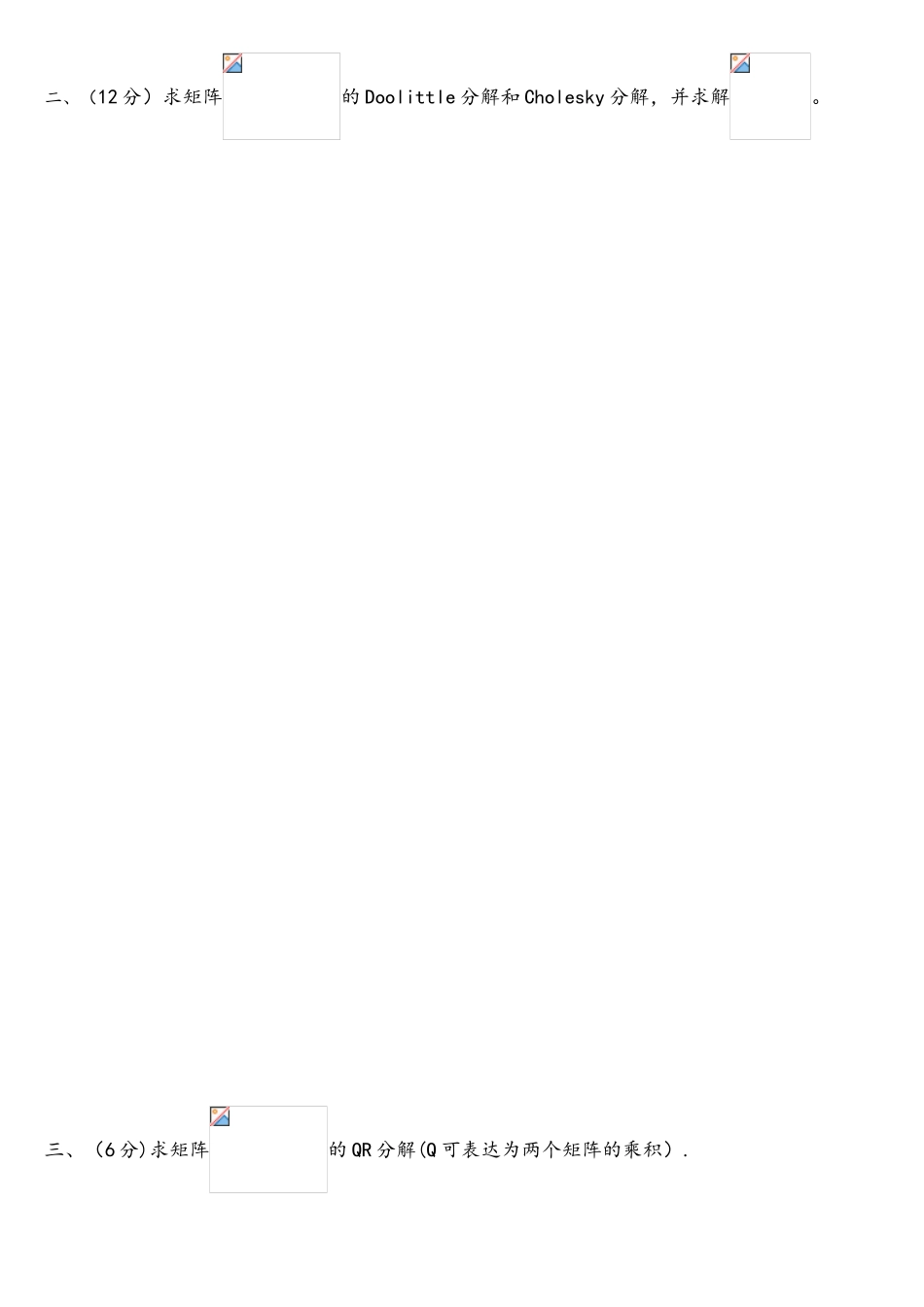
大 连 理 工 大 学 课 程 名 称: 计算措施 试卷: A 考试形式: 闭卷 讲课院(系): 数学系 考试日期: 年 12 月 12 日 试卷共 7 页 一二三四 五 六七总分原则分得 分装 一、填空(共 30 分,每空 1.5 分)(1)误差的来源重要有 、 、 、 。 (2)要使的近似值的相对误差限不超过,应至少取 位有效数字, 此时的近似值 = 。订 (3)设, 则= , = , = , = , 谱半径= , 2—条件数= , 奇异值为 。 线 (4)设,特征值,特征值 2 是半单的,而特征值 3 是亏损的,则 A 的 Jordan 原则型 . (5)已知,则 , .(6)求在附近的根的 Newton 迭代公式是: ,其收敛阶 。( 7) 计 算, 的 数 值 解 的 Euler 求 解 公 式 为 . 为使计算保持绝对稳定性, 步长 的取值范围 。二、(12 分)求矩阵的 Doolittle 分解和 Cholesky 分解,并求解。三、(6 分)求矩阵的 QR 分解(Q 可表达为两个矩阵的乘积).四、(12 分)根据迭代法对任意和均收敛的充要条件为, 证明若线性方程组中的为严格对角占优矩阵, 则 Jacobi 法和 G-S 法均收敛。五、(12 分)求满足下列插值条件的分段三次多项式(和), 并验证它是不是三次样条函数. , , , , ;, , , , .六、(10 分)证明线性二步法, 当时为二阶措施, 时为三阶措施, 并给出时的局部截断误差主项.七、(18 分)求上以为权函数的原则正交多项式系, , , 并由此求的二次最佳平方迫近多项式, 构造 Gauss 型求积公式, 并验证其代数精度。 大 连 理 工 大 学 课 程 名 称: 计算措施 试卷: A 考试形式: 闭卷 讲课院(系): 数学系 考试日期: 年 12 月 11 日 试卷共 8 页 一二三四 五 六七八总分原则分得 分装订 一、填空(共 30 分,每空 2 分)线 (1)误差的来源重要有 。 (2)按四舍五入的原则,取 具有四位有效数字的近似值= ,则绝对误差界为 ,相对误差界为 . ( 3) 矩 阵 算 子 范 数和 谱 半 径的 关 系 为 : , 和 . (4)设,特征值,特征值 2 是半单的,而特征值3 是亏损的,则 A 的 Jordan 原则型 。 (5)已知,则 , .(6)求在附近的根的 Newton 迭代公式是: .(7)使用 Aitken 加速迭代格式得到的 Steffensen 迭代格式为: ,对幂法数列的加速公式为: .(8)点 的 Newton—Cotes...