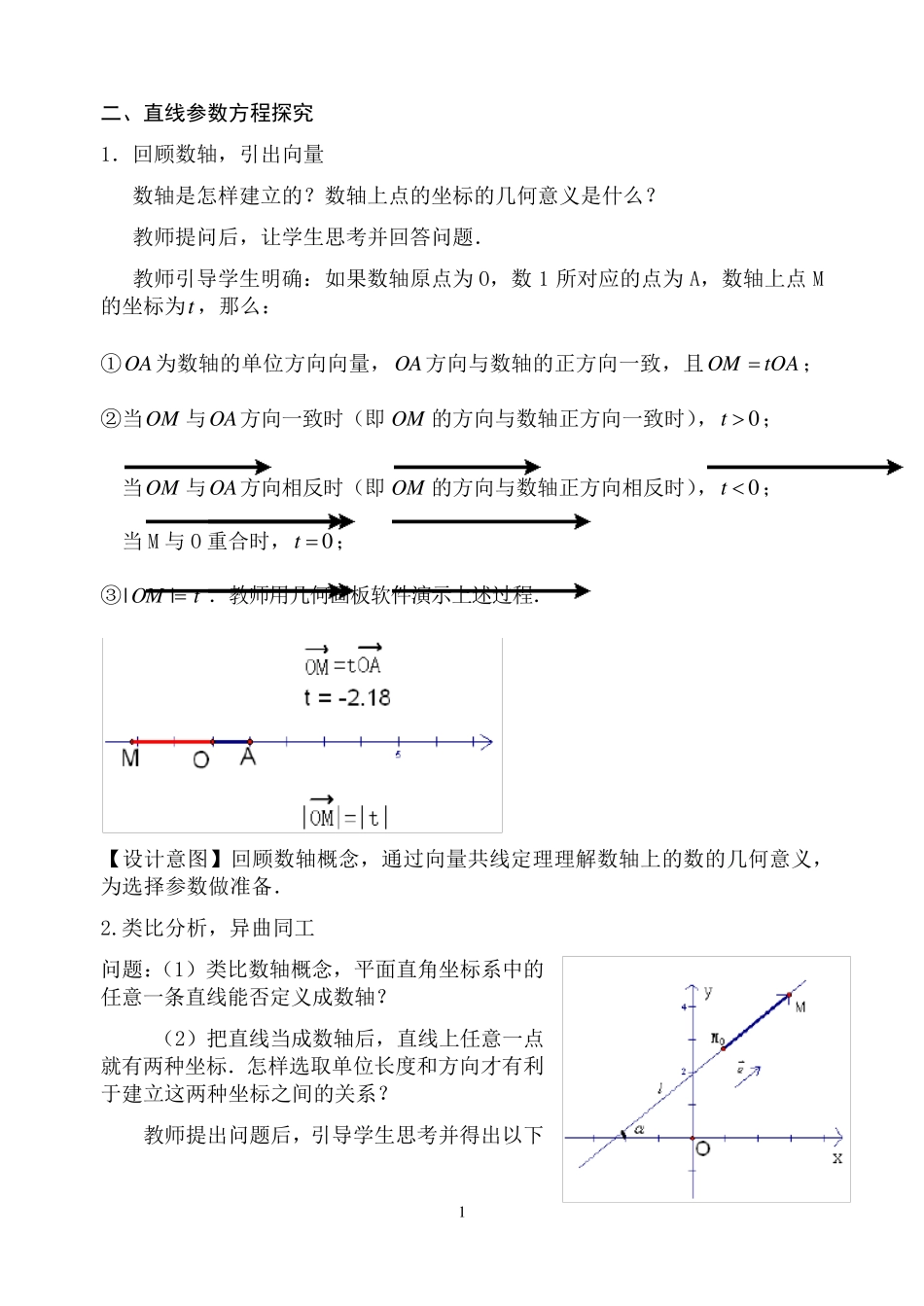
0 直线的参数方程 教学目标: 1 . 联系数轴、向量等知识,推导出直线的参数方程,并进行简单应用,体会直线参数方程在解决问题中的作用. 2 .通过直线参数方程的推导与应用,培养综合运用所学知识分析问题和解决问题的能力,进一步体会运动与变化、数形结合、转化、类比等数学思想. 3 . 通过建立直线参数方程的过程,激发求知欲,培养积极探索、勇于钻研 的科学精神、严谨的科学态度. 教学重点:联系数轴、向量等知识,写出直线的参数方程. 教学难点:通过向量法,建立参数t (数轴上的点坐标)与点在直角坐标系中的坐标 ,x y 之间的联系. 教学方式:启发、探究、交流与讨论. 教学手段:多媒体课件. 教学过程: 一、回忆旧知,做好铺垫 教师提出问题: 1.曲线参数方程的概念及圆与椭圆的参数方程. 2.直线的方向向量的概念. 3.在平面直角坐标系中,确定一条直线的几何条件是什么? 4.已知一条直线的倾斜角和所过的一个定点,请写出直线的方程. 5.如何建立直线的参数方程? 这些问题先由学生思考,回答,教师补充完善,问题 5 不急于让学生回答,先引起学生的思考. 【设计意图】通过回忆所学知识,为学生推导直线的参数方程做好准备. 1 二、直线参数方程探究 1.回顾数轴,引出向量 数轴是怎样建立的?数轴上点的坐标的几何意义是什么? 教师提问后,让学生思考并回答问题. 教师引导学生明确:如果数轴原点为O,数1 所对应的点为A,数轴上点M的坐标为t,那么: ①OA为数轴的单位方向向量,OA方向与数轴的正方向一致,且OMtOA;②当OM 与OA方向一致时(即 OM 的方向与数轴正方向一致时),0t; 当OM 与OA方向相反时(即 OM 的方向与数轴正方向相反时),0t; 当 M 与 O 重合时,0t; ③||OMt.教师用几何画板软件演示上述过程. 【设计意图】回顾数轴概念,通过向量共线定理理解数轴上的数的几何意义,为选择参数做准备. 2.类比分析,异曲同工 问题:(1)类比数轴概念,平面直角坐标系中的任意一条直线能否定义成数轴? (2)把直线当成数轴后,直线上任意一点就有两种坐标.怎样选取单位长度和方向才有利于建立这两种坐标之间的关系? 教师提出问题后,引导学生思考并得出以下 2 结论:选取直线l上的定点0M 为原点,与直线l平行且方向向上(l的倾斜角不为0 时)或向右(l的倾斜角为0 时)的单位向量e 确定直线l的正方向,同时在直线l上确定进行度量的单位长度...