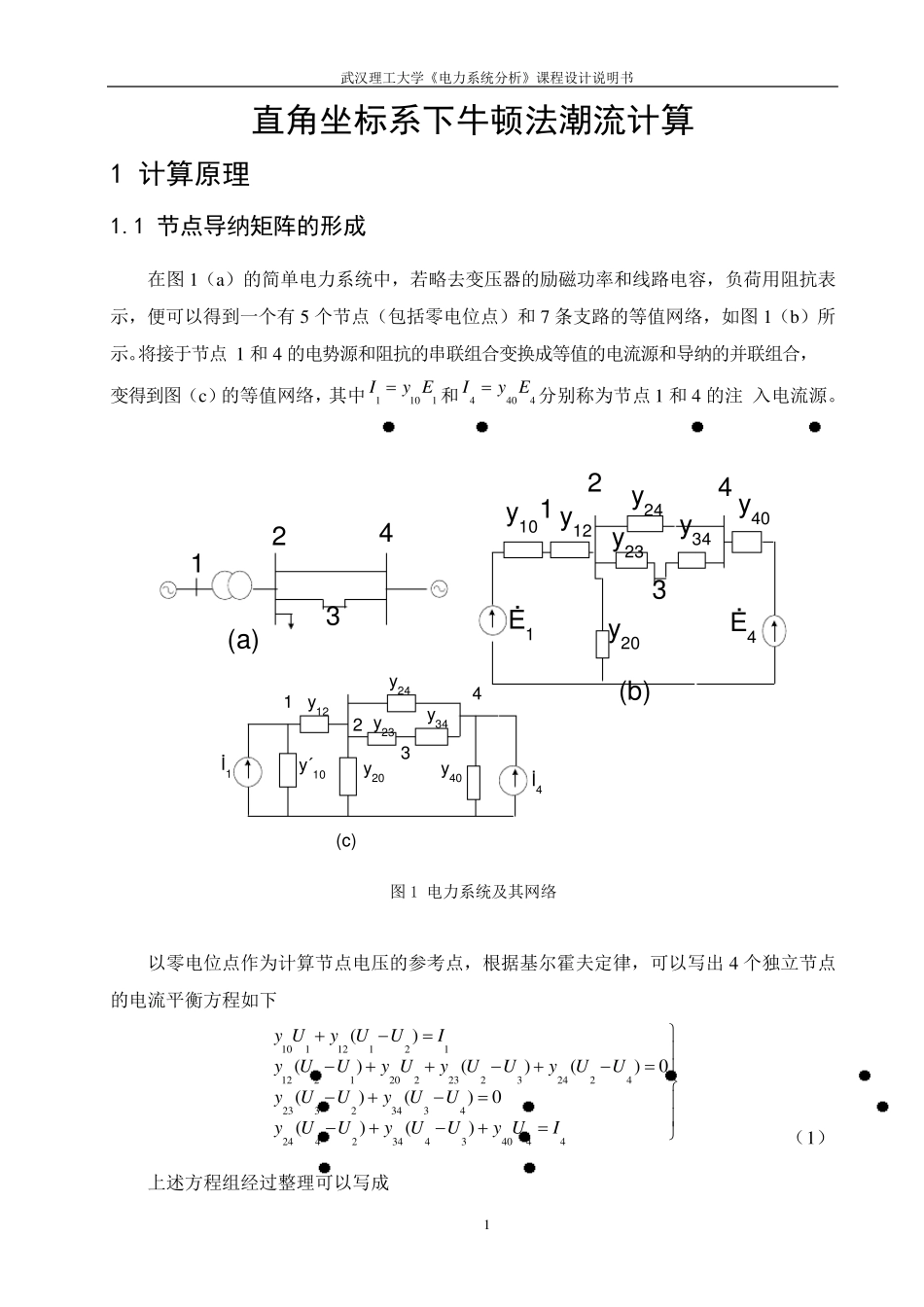
武汉理工大学《电力系统分析》课程设计说明书 1 直角坐标系下牛顿法潮流计算 1 计算原理 1.1 节点导纳矩阵的形成 在图1(a)的简单电力系统中,若略去变压器的励磁功率和线路电容,负荷用阻抗表示,便可以得到一个有5 个节点(包括零电位点)和7 条支路的等值网络,如图1(b)所示。将接于节点1 和4 的电势源和阻抗的串联组合变换成等值的电流源和导纳的并联组合,变得到图(c)的等值网络,其中1101Iy E和4404Iy E分别称为节点1 和4 的注 入电流源。 1243(a)Ė1Ė41234y10y12y24y20y23y34y40(b)İ1İ41234y12y24y23y34y40y20y´10(c) 图1 电力系统及其网络 以零电位点作为计算节点电压的参考点,根据基尔霍夫定律,可以写出 4 个独立节点的电流平衡方程如下 1011212112212022323242423323434244234434044()()()()0()()0()()y Uy UUIy UUy Uy UUy UUy UUy UUy UUy UUy UI (1) 上述方程组经过整理可以写成 武汉理工大学《电力系统分析》课程设计说明书 2 1 111 2212 112 222 332 443 223 333 444 224 334 44400Y UY UIY UY UY UY UY UY UY UY UY UY UI (2 ) 式中,1 11 01 2Yyy;2 22 02 32 41 2Yyyyy;3 32 33 4Yyy;4 44 02 43 4Yyyy;1 22 11 2YYy ;2 33 22 3YYy ;2 44 22 4YYy ;3 44 33 4YYy 。 一般的,对于有n 个独立节点的网络,可以列写n 个节点方程 1 111 22112 112 22221122nnnnnnnnnnY UY UY UIY UY UY UIY UY UY UI (3 ) 也可以用矩阵写成 111 11 212 12 222212nnnnnnnnUIYYYYYYUIYYYUI (4 ) 或缩写为 YUI (5 ) 矩阵Y 称为节点导纳矩阵。它的对角线元素iiY 称为节点i 的自导纳,其值等于接于节点i 的所有支路导纳之和。非对角线元素ijY 称为节点i 、 j 间的互导纳,它...