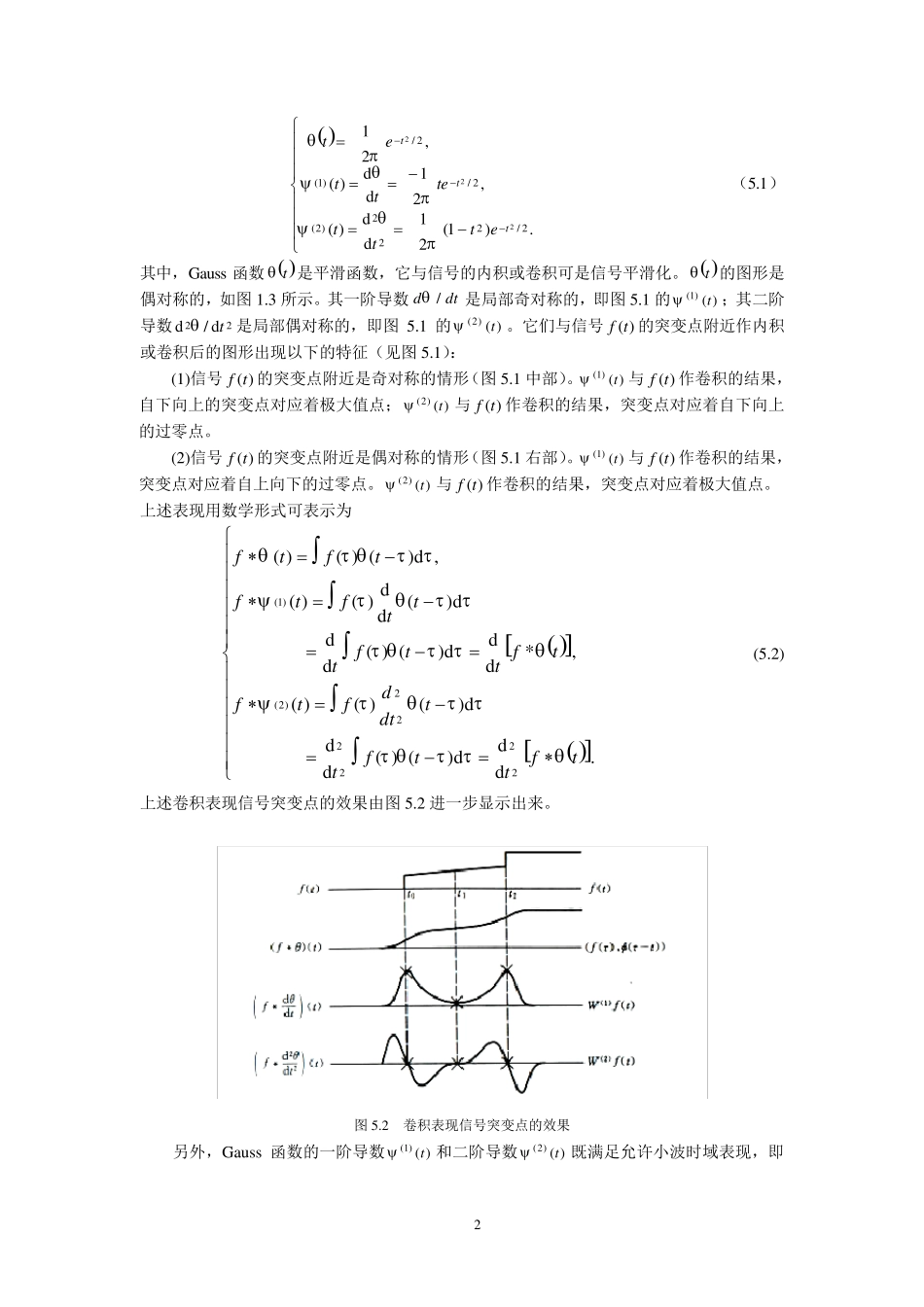
1 第5 章 小波分析在突变信号检测方面的应用 突变检测在数字信号处理中具有非常重要的地位和应用。在气象上,检测时间序列所涵有的突变或跃变,确定突变点,对分析各种尺度的气候变化具有重要的意义。小波变换在检测突变方面有很强的功能,因而得到广泛的应用。本章将介绍用小波分析方法检测突变信号的原理和方法。 5.1 检测信号突变点方法的原理 信号突变点的表现具有局部性。它可分为两类:一类是关于突变中心点局部奇对称的突变点,另一类是关于突变中心点局部偶对称的突变点。若用一个局部奇对称或一个局部偶对称的窗函数分别与这两类局部突变信号作卷积, 并在突变中心点附近的局部范围内观察卷积结果,则有如下规律: 局部奇*局部奇=局部偶, 局部奇*局部偶=局部奇, 局部偶*局部奇=局部奇, 局部偶*局部偶=局部偶。 现将局部信号的卷积效果示意于图 5.1 中。 图 5.1 内部卷积的局部极大值点,局部过零点与信号突变关系示意图 为了构造具有局部奇对称和局部偶对称的卷积函数,自然就想到 Gauss 函数及其导数 2 .)1(21dd)( ,21dd)( ,212/222)2(2/)1(2/222tttettttettet (5.1) 其中,Gauss 函数 t是平滑函数,它与信号的内积或卷积可是信号平滑化。 t的图形是偶对称的,如图 1.3 所示。其一阶导数dtd/是局部奇对称的,即图 5.1 的)()1(t;其二阶导数 22d/dt是局部偶对称的,即图 5.1 的)()2(t。它们与信号)(tf的突变点附近作内积或卷积后的图形出现以下的特征(见图 5.1): (1)信号)(tf的突变点附近是奇对称的情形(图 5.1 中部)。)()1(t与)(tf作卷积的结果,自下向上的突变点对应着极大值点;)()2(t与)(tf作卷积的结果,突变点对应着自下向上的过零点。 (2)信号)(tf的突变点附近是偶对称的情形(图 5.1 右部)。)()1(t与)(tf作卷积的结果,突变点对应着自上向下的过零点。)()2(t与)(tf作卷积的结果,突变点对应着极大值点。 上述表现用数学形式可表示为 . ddd)()(dd d)()()(, *ddd)()(dd d)(dd)()(,d)()()( 222222)2()1(tfttfttdtdftftfttftttftftftf (5.2) 上述卷积表现信号突变点的效果由图 5.2 进一步显示出来。 图 5.2 卷积...