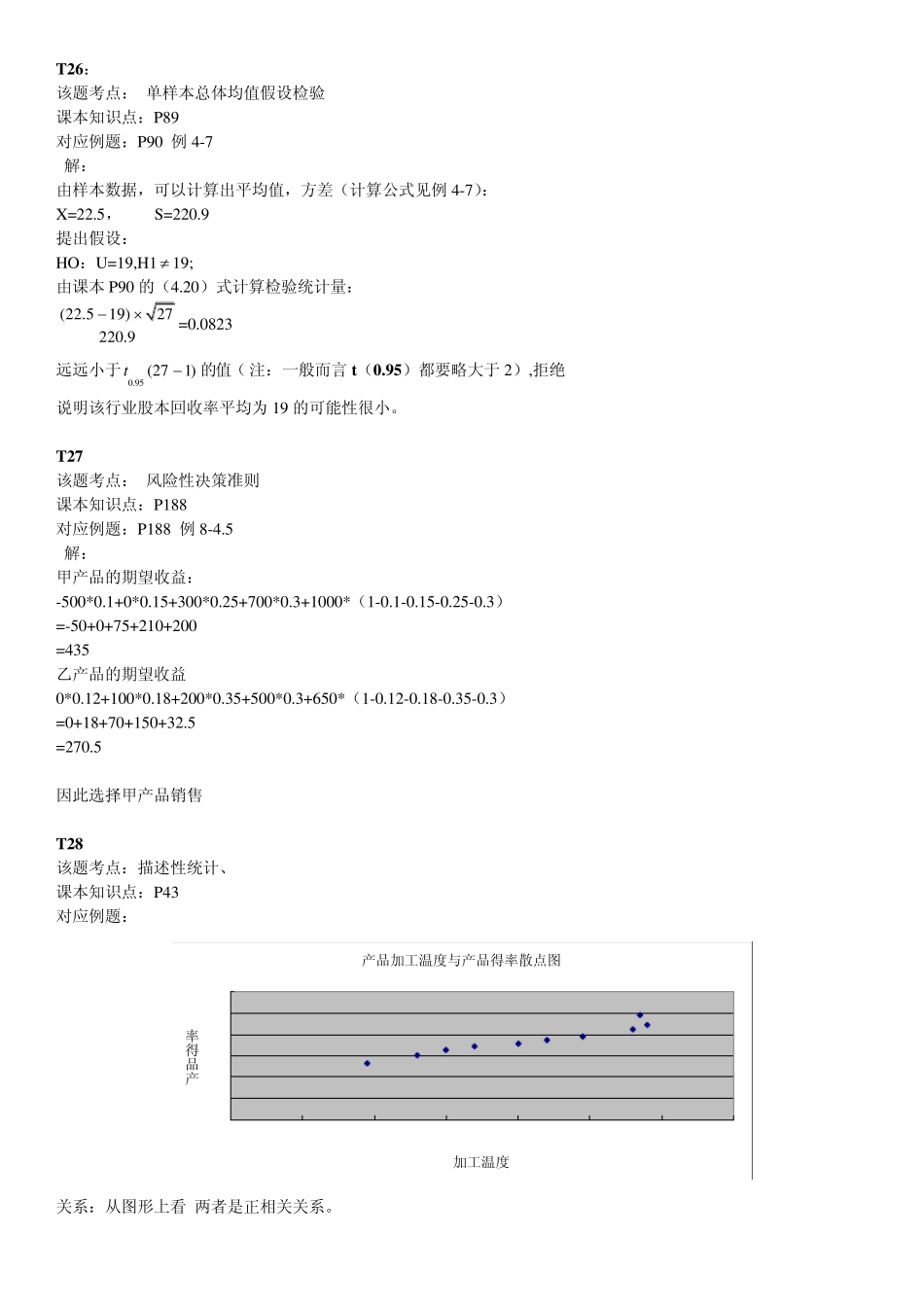
T26: 该题考点: 单样本总体均值假设检验 课本知识点:P89 对应例题:P90 例4-7 解: 由样本数据,可以计算出平均值,方差(计算公式见例4-7): X =22.5, S=220.9 提出假设: HO:U =19,H1 19; 由课本P90 的(4.20)式计算检验统计量: (22.519)27220.9=0.0823 远远小于0.95 (271)t的值(注:一般而言t(0.95)都要略大于2),拒绝 说明该行业股本回收率平均为19 的可能性很小。 T27 该题考点: 风险性决策准则 课本知识点:P188 对应例题:P188 例8-4.5 解: 甲产品的期望收益: -500*0.1+0*0.15+300*0.25+700*0.3+1000*(1-0.1-0.15-0.25-0.3) =-50+0+75+210+200 =435 乙产品的期望收益 0*0.12+100*0.18+200*0.35+500*0.3+650*(1-0.12-0.18-0.35-0.3) =0+18+70+150+32.5 =270.5 因此选择甲产品销售 T28 该题考点:描述性统计、 课本知识点:P43 对应例题: 产品加工温度与产品得率散点图051015202530010203040506070加工温度产品得率 关系:从图形上看 两者是正相关关系。 T 29 该题考点:单阶段离散型随机库存模型 课本知识点:P288 对应例题:P290 例12-6 解: Cu=零售价+缺货损失-购买单价 =0+1250-850 =400 Co=商品购买价格+存货费用-残值 =850+45-0 =895 计算得 Cu/(Cu+Co)=400/(400+895)=0.30888 计算累积概率: 需求量 80 90 100 110 120 概率 0.1 0.2 0.3 0.3 0.1 累计概率 0.1 0.3 0.6 0.9 1.0 由表可知,当需求量为100 时,累计概率0.6 大于转折概率0.30888,故经济订货量为100. T 30 该题考点:二人有限零和博弈 课本知识点:P321-P324 对应例题:例14-2,3,4 解 按1414max minijjia 计算局中人I 的收益,得到: a1:min{6,5,6,5}=5 a2:min{1,4,2,-1}=-1 a3:min{8,5,7,5}=5 a4:min{0,2,6,2}=6 因而1414max minijjia =max{5,-1,5,6}=5 说明局中人I 可以选择策略a1,也可以选择a3. 按14 14min maxijija 计算局中人II 的损失,得到: b1:max{6,1,8,0}=8 b2:max{5,4,5,2}=5; b3:max{6,2,7,6}=7; b4:max{5,-1,5,2}=5; 因而14 14min maxijija =min{8,5,7,5}=5 由于存在1414max minijjia =14 14min maxijija =5,该博弈值唯一,VG=5,纯策略意义下的解分别为 (a1,b2),(a1,b4),(a3,b2),(a3,b4) T 31 该题考点:线性规划问题...