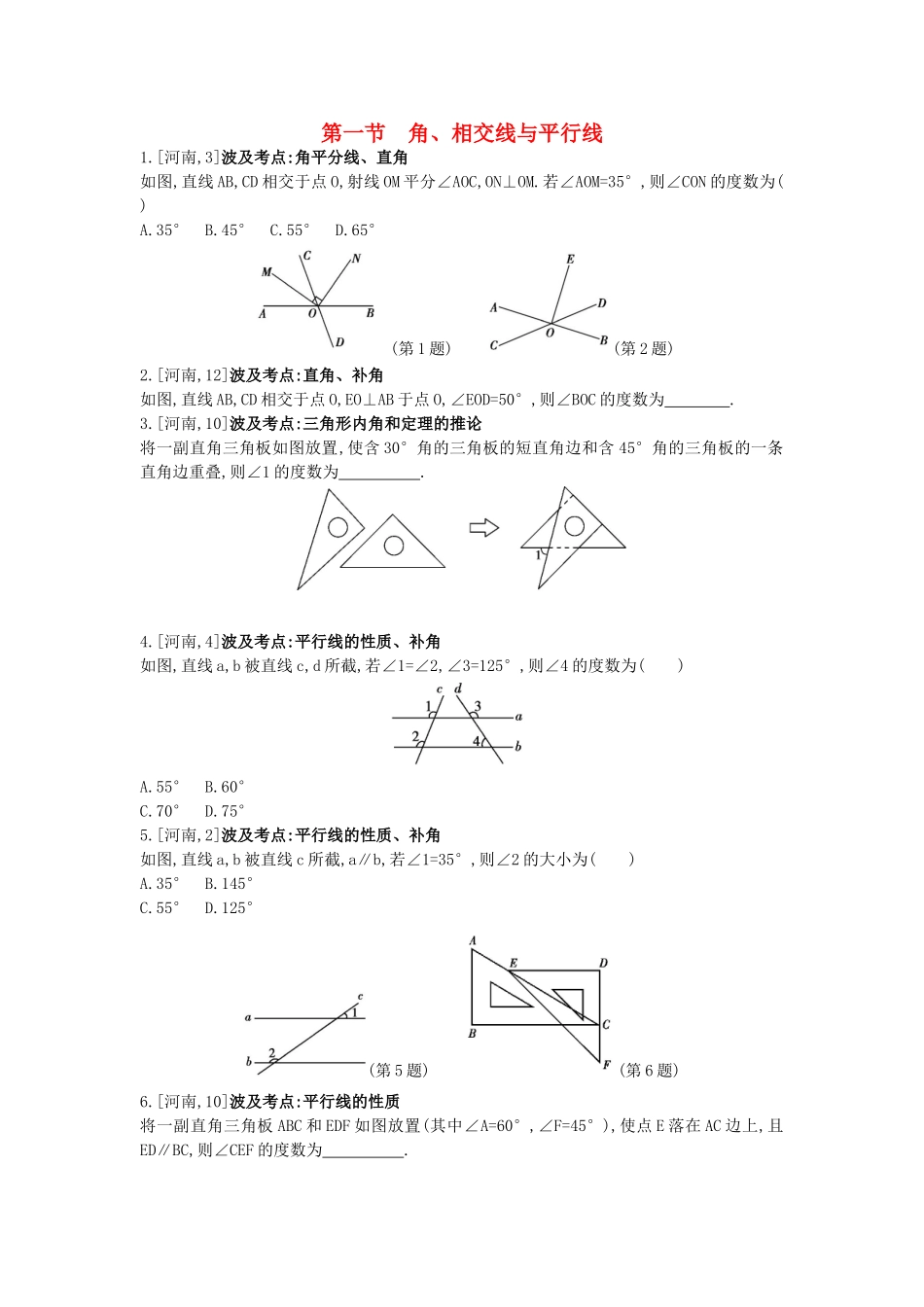
第一节 角、相交线与平行线1.[河南,3]波及考点:角平分线、直角如图,直线 AB,CD 相交于点 O,射线 OM 平分∠AOC,ON⊥OM.若∠AOM=35°,则∠CON 的度数为( )A.35°B.45°C.55°D.65°(第 1 题) (第 2 题)2.[河南,12]波及考点:直角、补角如图,直线 AB,CD 相交于点 O,EO⊥AB 于点 O,∠EOD=50°,则∠BOC 的度数为 . 3.[河南,10]波及考点:三角形内角和定理的推论将一副直角三角板如图放置,使含 30°角的三角板的短直角边和含 45°角的三角板的一条直角边重叠,则∠1 的度数为 . 4.[河南,4]波及考点:平行线的性质、补角如图,直线 a,b 被直线 c,d 所截,若∠1=∠2,∠3=125°,则∠4 的度数为( )A.55°B.60°C.70°D.75°5.[河南,2]波及考点:平行线的性质、补角如图,直线 a,b 被直线 c 所截,a∥b,若∠1=35°,则∠2 的大小为( )A.35°B.145°C.55°D.125°(第 5 题) (第 6 题)6.[河南,10]波及考点:平行线的性质将一副直角三角板 ABC 和 EDF 如图放置(其中∠A=60°,∠F=45°),使点 E 落在 AC 边上,且ED∥BC,则∠CEF 的度数为 . 第二节 三角形及其性质1.[河南,6]波及考点:垂直平分线、勾股定理、中位线如图,在△ABC 中,∠ACB=90°,AC=8,AB=10.DE 垂直平分 AC 交 AB 于点 E,则 DE 的长为( )A.6 B.5 C.4 D.3(第 1 题) (第 2 题)2.[河南,8]波及考点:等腰三角形的性质、角平分线如图,在△ABC 中,AB=AC,CD 平分∠ACB,∠A=36°,则∠BDC 的度数为 . 3.[河南,15]波及考点:折叠、勾股定理如图,在 Rt△ABC 中,∠A=90°,AB=AC,BC=+1,点 M,N 分别是边 BC,AB 上的动点,沿 MN 所在的直线折叠∠B,使点 B 的对应点 B'一直落在边 AC 上.若△MB'C 为直角三角形,则 BM 的长为 . 4.[河南,15]波及考点:折叠、三角函数如图,在 Rt△ABC 中,∠ACB=90°,∠B=30°,BC=3.点 D 是 BC 边上一动点 (不与点 B,C 重叠)过点 D 作 DE⊥BC 交 AB 边于点 E,将∠B 沿直线 DE 翻折,点 B 落在射线 BC 上的点 F 处.当△AEF 为直角三角形时,BD 的长为 . 5.[河南,15]波及考点:切线、三角函数如图,Rt△ABC 中,∠C=90°,∠ABC=30°,AB=6,点 D 在 AB 边上,点 E 是 BC 边上一点(不与点B,C 重叠),且 DA=DE,则 AD 的取值范围是 . 第三节 全等三角形1.[河南,17]波及考点:全等三角形的判定与性质、垂直平分线如图所示,∠BAC=∠ABD,AC=BD,点 O 是 AD,BC 的交点,点 ...