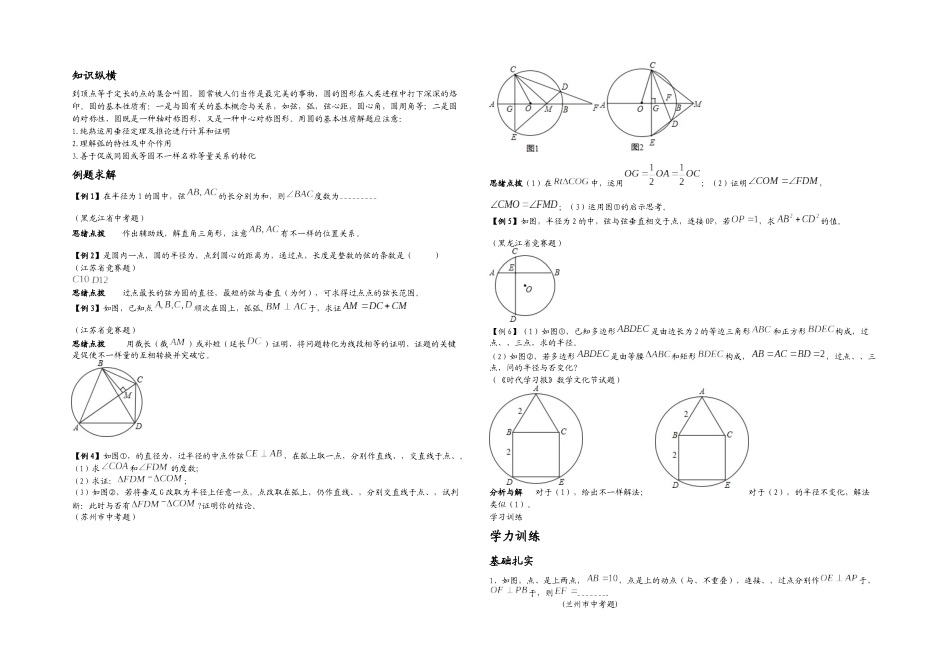
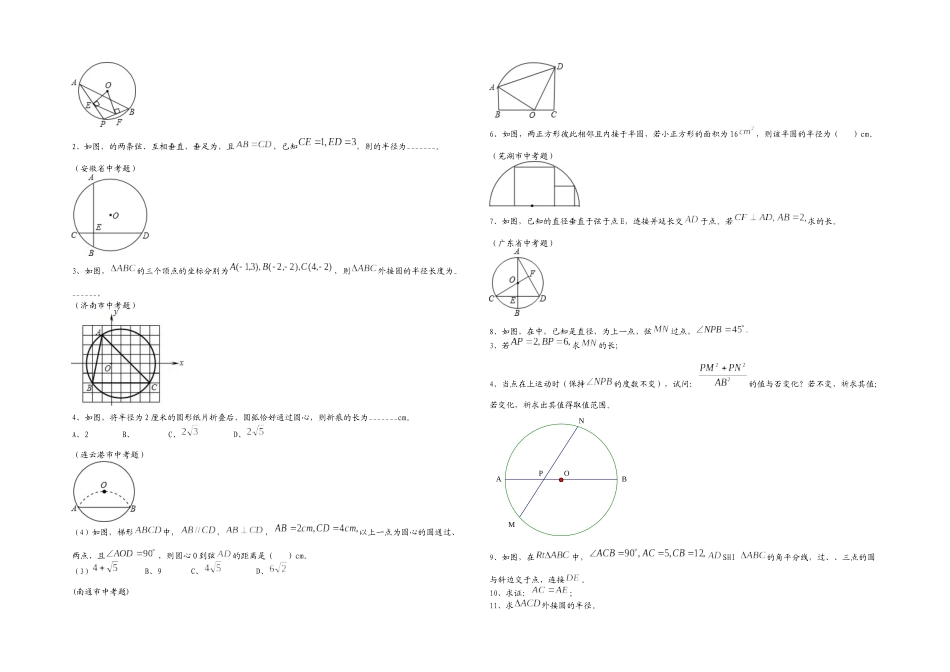
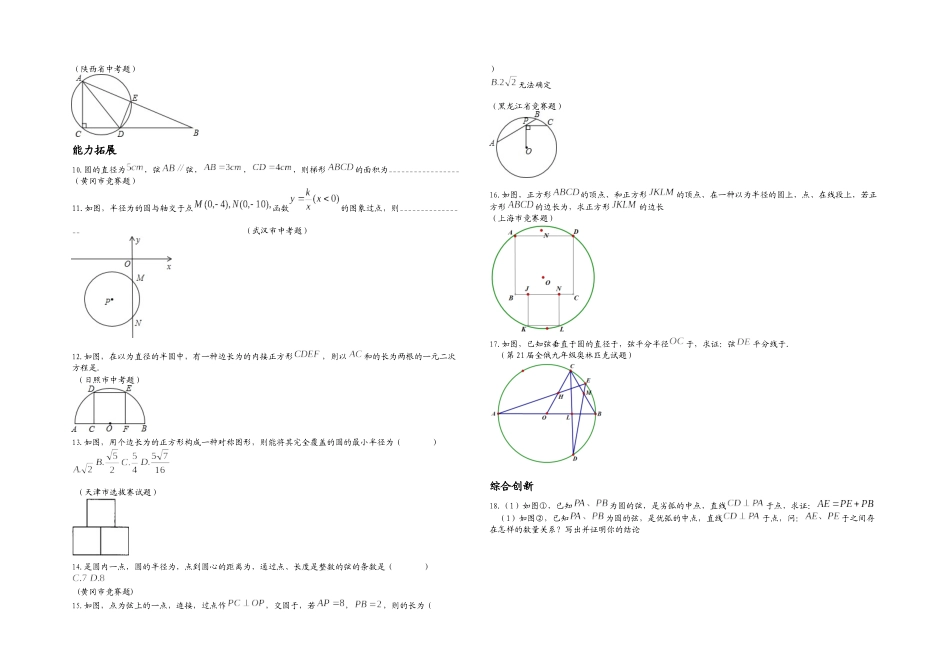
知识纵横到顶点等于定长的点的集合叫圆,圆常被人们当作是最完美的事物,圆的图形在人类进程中打下深深的烙印。圆的基本性质有:一是与圆有关的基本概念与关系,如弦,弧,弦心距,圆心角,圆周角等;二是圆的对称性,圆既是一种轴对称图形,又是一种中心对称图形。用圆的基本性质解题应注意:1.纯熟运用垂径定理及推论进行计算和证明2.理解弧的特性及中介作用3.善于促成同圆或等圆不一样名称等量关系的转化例题求解【例 1】在半径为 1 的圆中,弦的长分别为和,则度数为_________(黑龙江省中考题)思绪点拨 作出辅助线,解直角三角形,注意有不一样的位置关系。【例 2】是圆内一点,圆的半径为,点到圆心的距离为,通过点,长度是整数的弦的条数是( ) (江苏省竞赛题)思绪点拨 过点最长的弦为圆的直径,最短的弦与垂直(为何),可求得过点点的弦长范围。【例 3】如图,已知点顺次在圆上,弧弧,于,求证(江苏省竞赛题)思绪点拨 用截长(截)或补短(延长)证明,将问题转化为线段相等的证明,证题的关键是促使不一样量的互相转换并突破它。【例 4】如图,的直径为,过半径的中点作弦,在弧上取一点,分别作直线、,交直线于点、。(1)求和的度数;(2)求证:~;(3)如图,若将垂足 G 改取为半径上任意一点,点改取在弧上,仍作直线、,分别交直线于点、,试判断:此时与否有~?证明你的结论。(苏州市中考题)思绪点拨(1)在中,运用;(2)证明,;(3)运用图的启示思考。【例 5】如图,半径为 2 的中,弦与弦垂直相交于点,连接 OP,若,求的值。(黑龙江省竞赛题)【例 6】(1)如图,已知多边形是由边长为 2 的等边三角形和正方形构成,过点、、三点,求的半径。(2)如图,若多边形是由等腰和矩形构成,,过点、、三点,问的半径与否变化?(《时代学习报》数学文化节试题)分析与解 对于(1),给出不一样解法;对于(2),的半径不变化,解法类似(1)。学习训练学力训练基础扎实1、如图,点、是上两点,,点是上的动点(与、不重叠),连接、,过点分别作于,于,则_______. (兰州市中考题)2、如图,的两条弦、互相垂直,垂足为,且,已知,则的半径为_______。(安徽省中考题)3、如图,的三个顶点的坐标分别为,则外接圆的半径长度为_______。(济南市中考题)4、如图,将半径为 2 厘米的圆形纸片折叠后,圆弧恰好通过圆心,则折痕的长为_______cm。A、2 B、 C、 D、(连云港市中考题)...