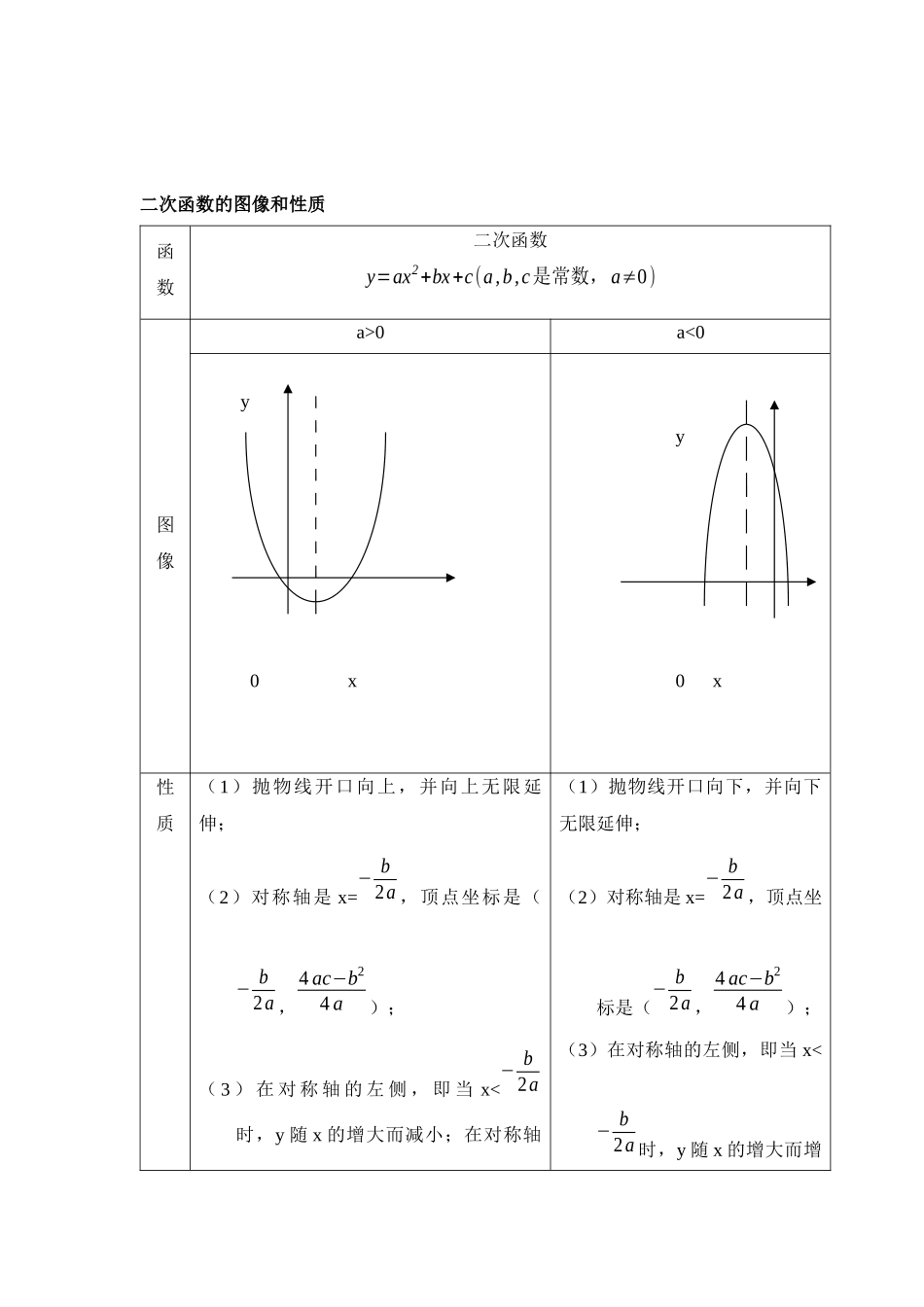
二次函数综合知识定位函数是我们讨论两变量之间关系的一个工具,到高中后更是数学学科中的重点及难点。而在初中阶段,二次函数是作为我们的必考内容和重难点。在填空和选择部分提出会考察二次函数的定义、图像及其性质、平移;解答部分通常会作为我们小压轴题的命题背景,与动点构成的相似三角形、等腰三角形相结合。知识梳理二次函数的图像和二次函数图像的画法二次函数的图像是一条关于x=− b2a 对称的曲线,这条曲线叫抛物线。抛物线的主要特征:①有开口方向;②有对称轴;③有顶点。五点法:1、先根据函数解析式,求出顶点坐标,在平面直角坐标系中描出顶点 M,并用虚线画出对称轴2、求抛物线y=ax2+bx+c 与坐标轴的交点:当抛物线与 x 轴有两个交点时,描出这两个交点 A,B 及抛物线与 y 轴的交点C,再找到点 C 的对称点 D。将这五个点按从左到右的顺序连接起来,并向上或向下延伸,就得到二次函数的图像。当抛物线与 x 轴只有一个交点或无交点时,描出抛物线与 y 轴的交点 C 及对称点 D。由 C、M、D 三点可粗略地画出二次函数的草图。假如需要画出比较精确的图像,可再描出一对对称点 A、B,然后顺次连接五点,画出二次函数的图像。二次函数的图像和性质函数二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图像a>0a<0 y 0 x y 0 x 性质(1)抛物线开口向上,并向上无限延伸;(2)对称轴是 x=− b2a ,顶点坐标是(− b2a ,4 ac−b24 a);( 3 ) 在 对 称 轴 的 左 侧 , 即 当 x<− b2a时,y 随 x 的增大而减小;在对称轴(1)抛物线开口向下,并向下无限延伸;(2)对称轴是 x=− b2a ,顶点坐标是(− b2a ,4 ac−b24 a);(3)在对称轴的左侧,即当 x<− b2a 时,y 随 x 的增大而增的右侧,即当 x>− b2a 时,y 随 x 的增大而增大,简记左减右增;(4)抛物线有最低点,当 x=− b2a 时,y有最小值,y最小值=4ac−b24 a大;在对称轴的右侧,即当x>− b2a 时,y 随 x 的增大而减小,简记左增右减;(4)抛物线有最高点,当 x=− b2a 时 , y 有 最 大 值 ,y最大值=4ac−b24 a二次函数图像的应用二次函数的图像可以和一元二次方程、几何等结合起来考察,需要我们在熟悉二次函数的基础上完成转化。例题精讲【题目】在实验中我们常常采纳计算机在平面直角坐标系中画出抛物线 y=x2和直线y=−x+3 ,利用两图像交点的横坐标来求一元二次方程x2+x−...