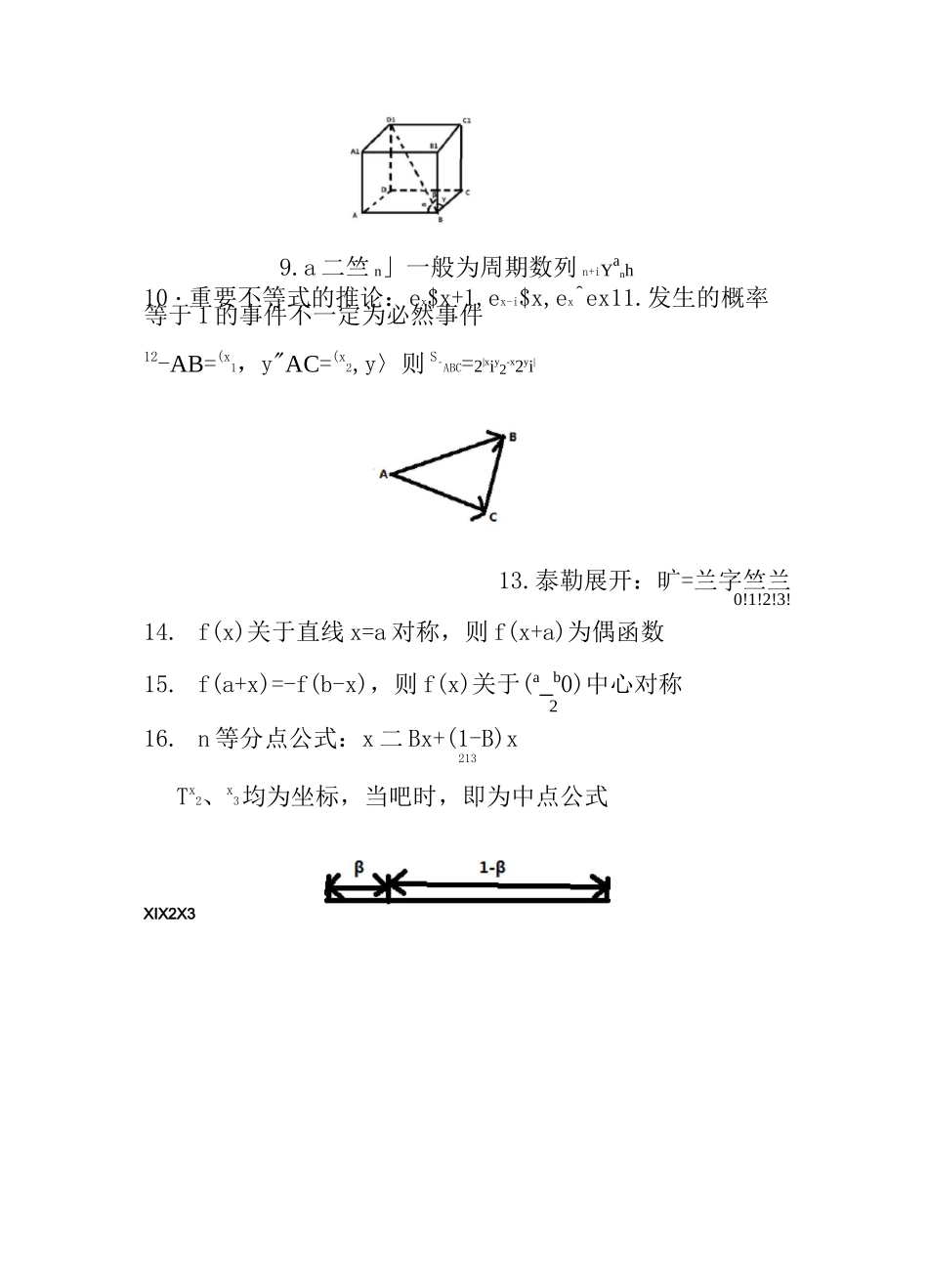
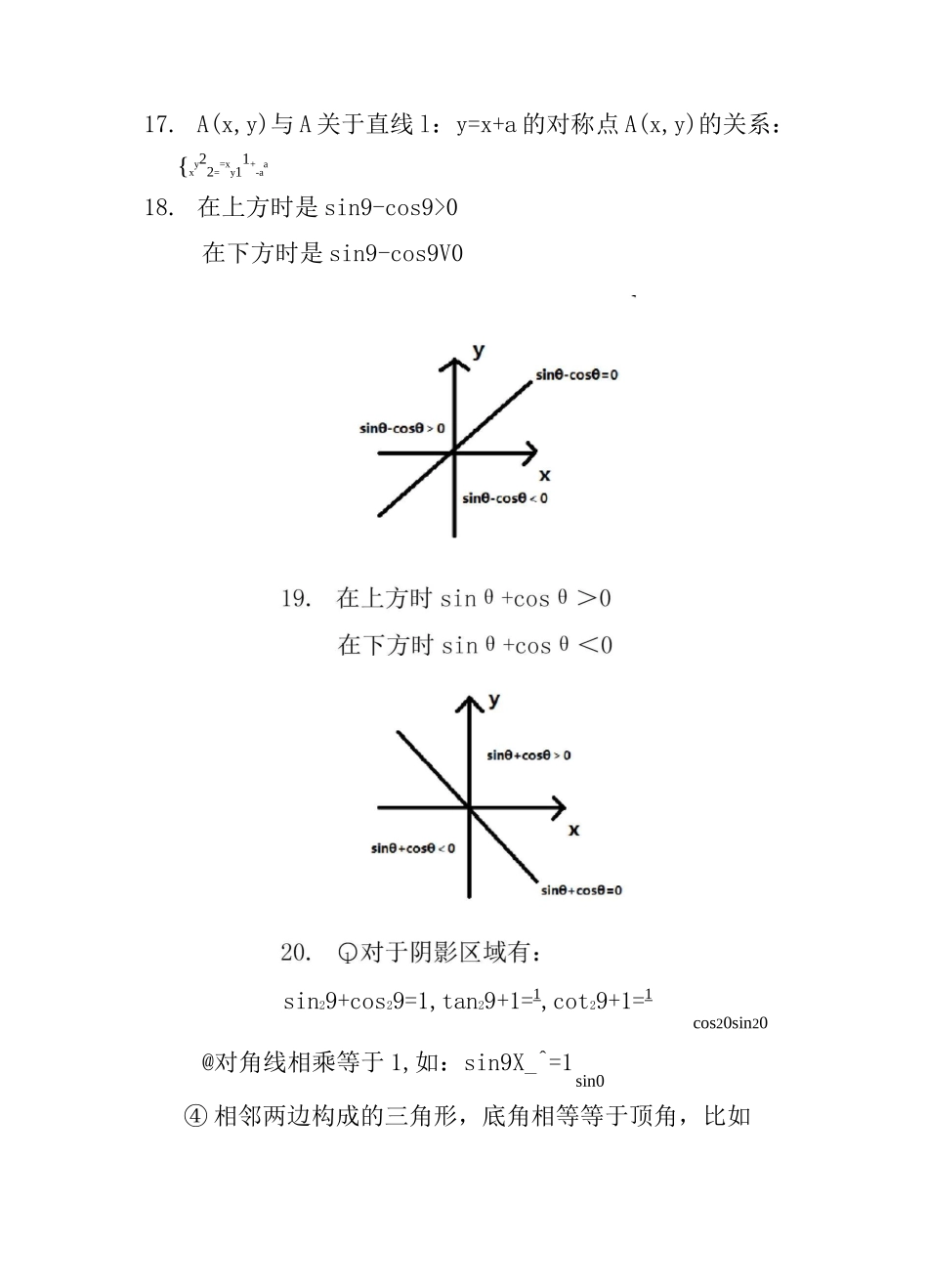
1. 常见的数值:e~2.72,V2^1.41,血〜1.73ln2~0.69,ln3~1.102. 类似“Vn+1-1”的式子都可以写成 n 项和的形式,在一些证明题中会有应用:Vn+lT=(Vn+1-Vn)+(Vn-Vn—1)+...+(V2-VDE—(Vt+1 一 Vk)k=13. 几何平均不等式:Sn=1a{2nVa1a2a3^an4. 组合数的性质:Nf+CfT组合数性质的推论:cn+cn+i+…+cn+m=Cn+m+i5. 正四面体中,外接球半径:内接球半径=3:16. 圆台的侧面积:S=n(r+r)l(r、r 为上下底圆的半侧 11径,l 为母线长。特殊的,当 r=0 时,即为圆锥时,有1S=nrl)侧7. 圆台的体积公式:V=1(S+VSS1+S.)h3118. 矩形 ABCD 的对角线 AC 与 BC、CD 所成的角分别为 a、B,则有 sin2a+sin2B=1则有 cos2a+cos2B+cos2Y=1sin2a+sin2B+sin2Y=29.a 二竺 n」一般为周期数列 n+iYanh10・重要不等式的推论:ex$x+1,ex-i$x,ex^ex11.发生的概率等于 1 的事件不一定为必然事件12-AB=(x1,y"AC=(x2,y〉则 S^ABC=2|xiy2-x2yi|13.泰勒展开:旷=兰字竺兰0!1!2!3!14. f(x)关于直线 x=a 对称,则 f(x+a)为偶函数15. f(a+x)=-f(b-x),则 f(x)关于(a_b0)中心对称216. n 等分点公式:x 二 Bx+(1-B)x213Tx2、x3均为坐标,当吧时,即为中点公式XIX2X317. A(x,y)与 A 关于直线 l:y=x+a 的对称点 A(x,y)的关系:{xy22==xy11+-aa18. 在上方时是 sin9-cos9>0在下方时是 sin9-cos9V0sin29+cos29=1,tan29+1=1,cot29+1=1cos20sin20@对角线相乘等于 1,如:sin9X_^=1sin0④ 相邻两边构成的三角形,底角相等等于顶角,比如26.+f(X3)+f(X4)]cos9X1=cot9sin021.若 f(x)是[a,b]上的凸函数,则对不相等的 x,x,x,123[a,b]则有:f(X 1 +X 2 +X 3 +X 4 )〉1[f(X)+f(X)441222. (x-a)2+(lnx-2a)2具有几何意义:表示(x,lnx)与(a,2a)两点间的距离平方23. 在证明题中,1+土+丄+・・・+丄通常进行裂项处理2232n224. g(x)=eX-1为奇函数ex+125. sin2a=2t,cos2a=1-t2,tan2a=2t,(t 二 tana)1+t21+t21-t2tar)a=1-cosa二 sina2sina1+cosa27.1±sin2a=(sina±cosa)228.若 a+B=45°,则有(1+tana)(1+tanB)=2i-OG》》》35.若 P、G、Q 三点共线,则有 OP=gG+(1-u)T0Q(即后面系数和要为 1),其中□二丄,1-卩=^129.类似 cos20°cos40°cos60°cos80°这样 cos 连乘的式子,且角度为公比为 2 的等比数列,可采用同时乘除sinB 的形式,连续用倍角公式30. 在厶 ABC 中,A(x,y),B(x,y),C(x,y),则厶112233ABC 的重心 O 为(X...