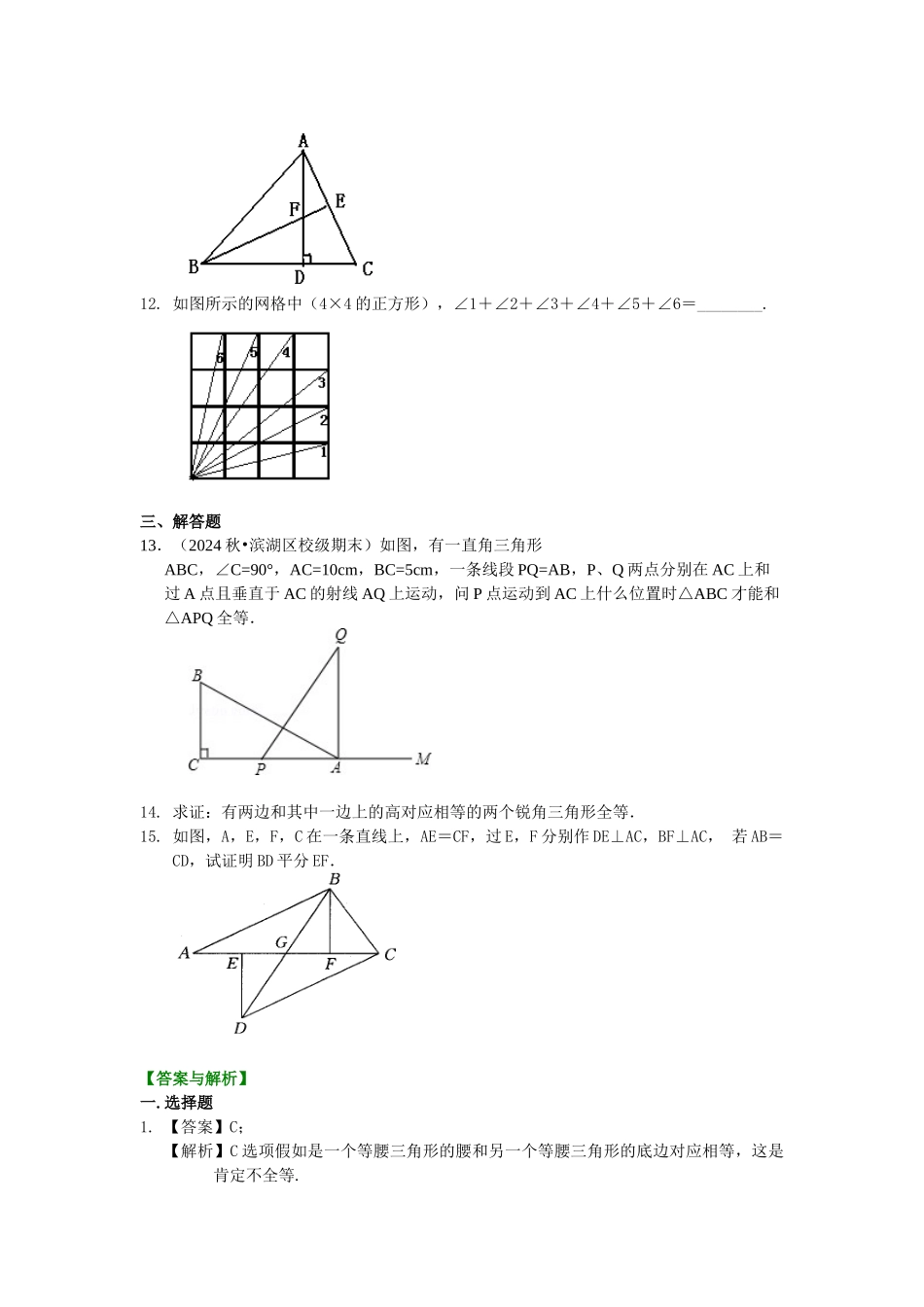
【巩固练习】一、选择题1.下列命题中,不正确的是( ) A.斜边对应相等的两个等腰直角三角形全等B.两条直角边对应相等的两个直角三角形全等C.有一条边相等的两个等腰直角三角形全等D.有一条直角边和斜边上的中线对应相等的两个直角三角形全等2. 如图,△ABC 中,AB=AC,BD⊥AC 于 D,CE⊥AB 于 E,BD 和 CE 交于点 O,AO 的延长线交BC 于 F,则图中全等直角三角形的对数为( ) A. 3 对 B. 4 对 C. 5 对 D. 6 对3. 如图,在△ABC 中 AD⊥BC,CE⊥AB,垂足分别为 D、E,AD、CE 交于点 H,已知 EH=EB=3,AE=4,则 CH 的长是( )A.1 B.2 C.3 D.44. 在如图中,AB=AC,BE⊥AC 于 E,CF⊥AB 于 F,BE、CF 交于点 D,则下列结论中不正确的是( ) A. △ABE≌△ACF B. 点 D 在∠BAC 的平分线上C. △BDF≌△CDE D. 点 D 是 BE 的中点5.(2024 春•泰山区期末)如图所示,∠C=∠D=90°添加一个条件,可使用“HL”判定Rt△ABC 与 Rt△ABD 全等.以下给出的条件适合的是( )A.AC=ADB.AB=ABC.∠ABC=∠ABDD.∠BAC=∠BAD6. 已知如图,AD∥BC,AB⊥BC,CD⊥DE,CD=ED,AD=2,BC=3,则△ADE 的面积为( ) A. 1 B. 2 C. 5 D. 无法确定 二、填空题7. 如图,E、B、F、C 在同一条直线上,若∠D=∠A=90°,EB=FC,AB=DF.则ΔABC≌_____,全等的根据是_____.8. (2024 秋•亭湖区校级月考)如图,AB=AC,CD⊥AB 于点 D,BE⊥AC 于点 E,BE与 CD 相交于点 O,图中有 对全等的直角三角形.9. 判定两直角三角形全等的各种条件:(1)一锐角和一边;(2)两边对应相等;(3)两锐角对应相等.其中能得到两个直角三角形全等的条件是_________.10. 如图,△ABC 中,AM 平分∠CAB,CM=20,那么 M 到 AB 的距离是_________.11. 如图,已知 AD 是△ABC 的高,E 为 AC 上一点,BE 交 AD 于 F,且 BF=AC,FD=CD.则∠BAD=_______.cmcm12. 如图所示的网格中(4×4 的正方形),∠1+∠2+∠3+∠4+∠5+∠6=________. 三、解答题13.(2024 秋•滨湖区校级期末)如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段 PQ=AB,P、Q 两点分别在 AC 上和过 A 点且垂直于 AC 的射线 AQ 上运动,问 P 点运动到 AC 上什么位置时△ABC 才能和△APQ 全等.14. 求证:有两边和其中一边上的高对应相等的两个锐角三角...