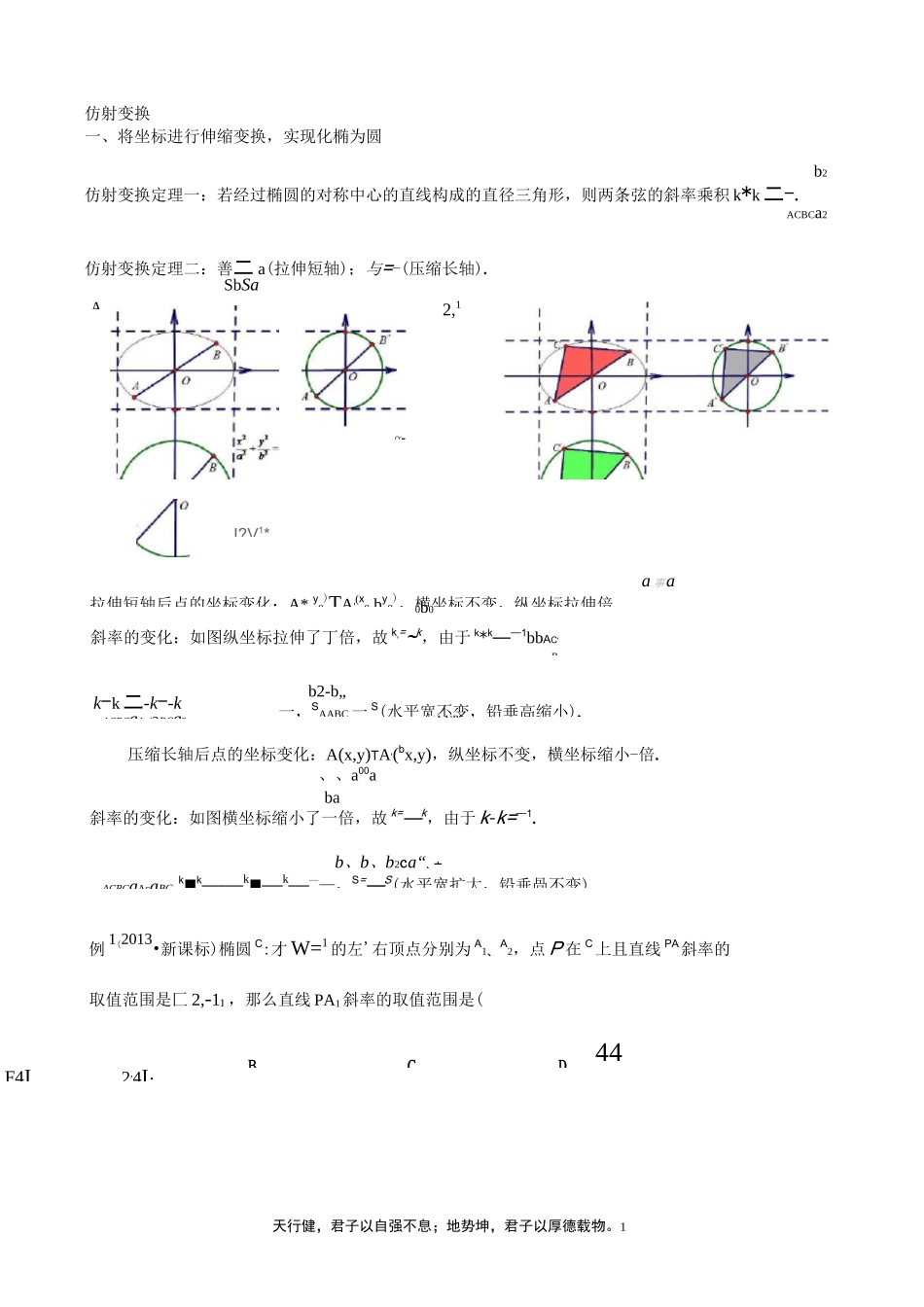
44天行健,君子以自强不息;地势坤,君子以厚德载物。1I?V1*a 事a拉伸短轴后点的坐标变化:A*,yo)TA'(xo,byo),横坐标不变,纵坐标拉伸倍.0b0斜率的变化:如图纵坐标拉伸了丁倍,故 k'=~k,由于 k*k——1bbAC'Bk-k 二-k--kACBCaAc'aBCa2b2-b„一,SAABC 一 S(水平宽不变,铅垂高缩小).AA'B'压缩长轴后点的坐标变化:A(x,y)TA'(bx,y),纵坐标不变,横坐标缩小-倍.、、a00aba斜率的变化:如图横坐标缩小了一倍,故 k=—k,由于 k-k=—1.b、b、b2ca“、亠k■k——k■—k———,S=—S(水平宽扩大,铅垂咼不变).ACBCaAcaBC例 1(2013•新课标)椭圆 C:才 W=1的左'右顶点分别为 A1、A2,点 P 在 C上且直线 PA斜率的取值范围是匚 2,-1],那么直线 PA1斜率的取值范围是(A.2,4I;BF4IC2,1D仿射变换一、将坐标进行伸缩变换,实现化椭为圆b2仿射变换定理一:若经过椭圆的对称中心的直线构成的直径三角形,则两条弦的斜率乘积 k*k 二-.ACBCa2仿射变换定理二:善二 a(拉伸短轴);与=-(压缩长轴).SbSaO'■韧44天行健,君子以自强不息;地势坤,君子以厚德载物。2x2y2韧天行健,君子以自强不息;地势坤,君子以厚德载物。3隹直线 AF 的斜率0为坐标原点.(1) 求 E 的方程;豪 I(2) 设过点 A 的直线 l 与 E 相交于 P、Q 两点,当 AOPQ 的面积最大时,求 l 的方程.二、椭圆的角平分线定理X2y2仿射变换定理三:若点 A,B 是椭圆一+1 二 1(a>b>0)上的点,AB 与椭圆长轴交点为 N,在长轴上a2b2一定存在一个点 M,当且仅当 x•x 二 a2时,ZAMN=ZBMN,即长轴为角平分线.MNx2y2若点 A,B 是椭圆一+^=1(a>b>0)上的点,AB 与椭圆短轴交点为 N,在短轴上一定存在一个点 M,a2b2当且仅当 y•y 二 b2时,ZAMN=/BMN,即短轴为角平分线.MN韧天行健,君子以自强不息;地势坤,君子以厚德载物。4例 4(2018・全国卷 I)设椭圆 C••下+y2二 1 的右焦点为 F,过 F 的直线 l 与 C 交于 A,B 两点,点 M 的坐标为(2,0).(1)当 l 与 x 轴垂直时,求直线 AM 的方程;(2)设 O 为坐标原点,证明:三、仿射变换定理四:若以椭圆石+厉二 1的对称中心引出两条直线交椭圆于 A,B两点,且 kOAk则经过仿射变换后 k•k=-1,所以 S 为定值.OA'OB'AAOBX2y2仿射变换定理五:若椭圆-+厉二 1上三点 A,B,M,满足① kOAkOBb2—_:②cabSAAOB=T;OM=sina-OA+cosa•OB,(ae例 5(2011•山东)已知直线 1 与...