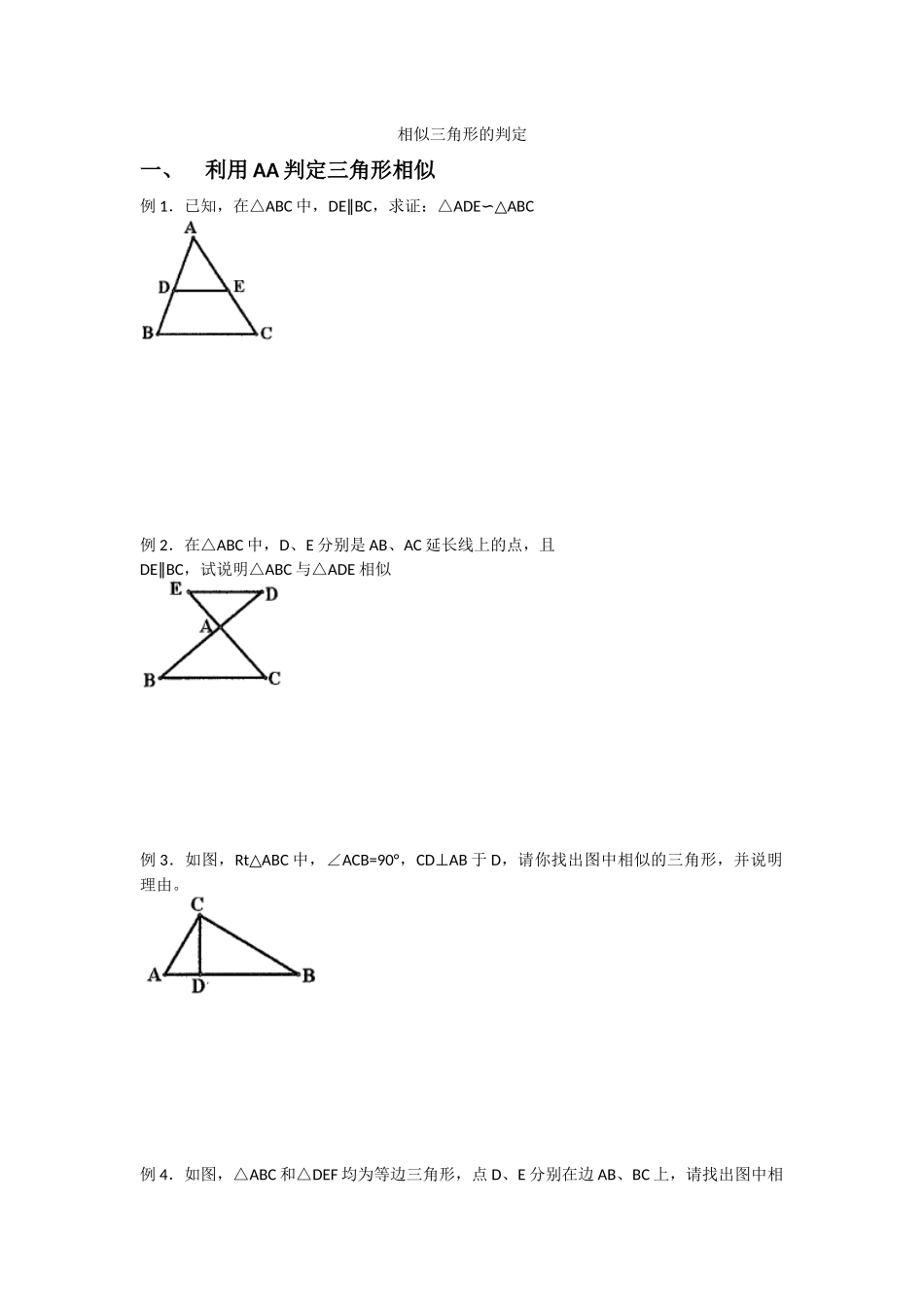
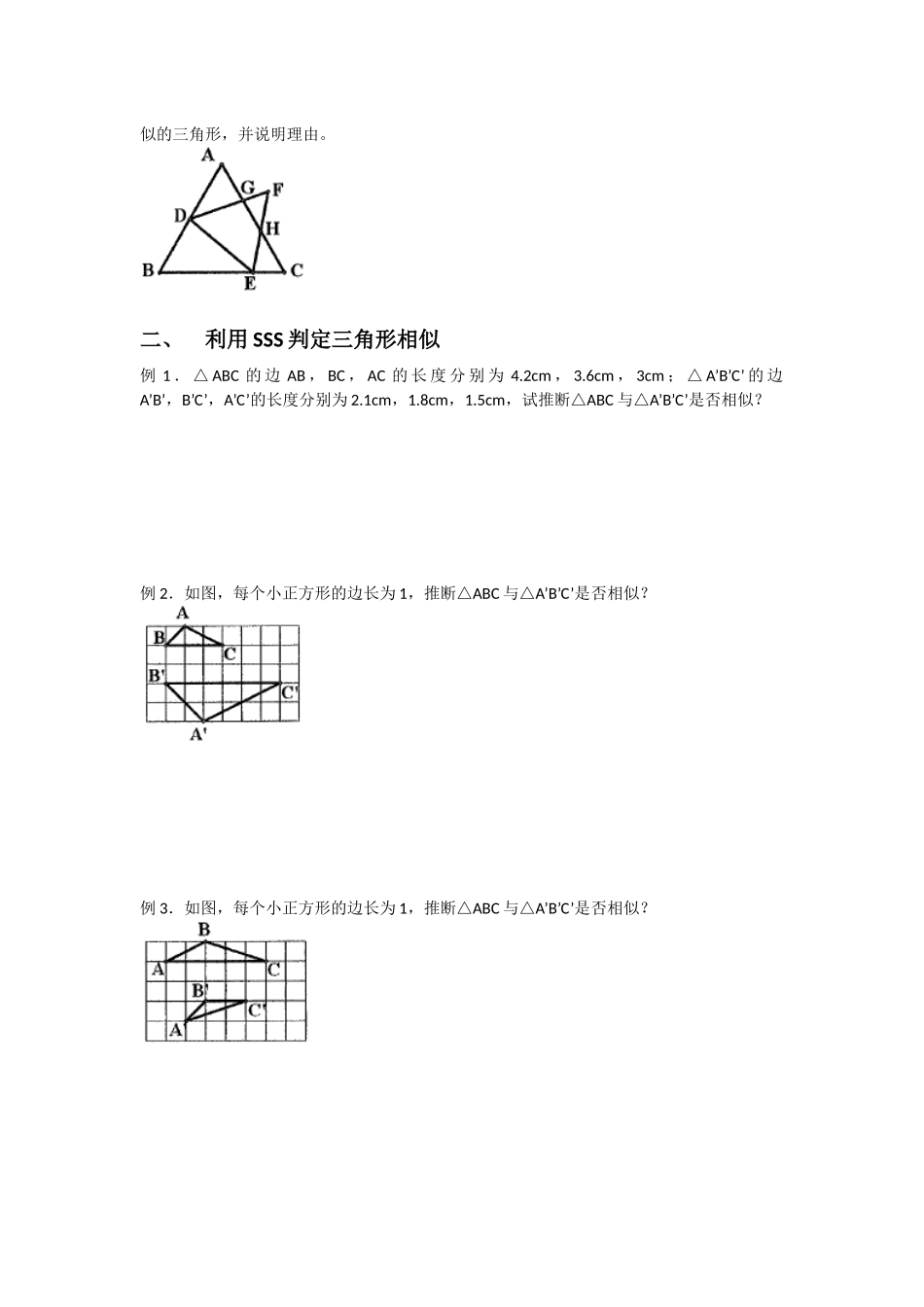
相似三角形的判定一、利用 AA 判定三角形相似例 1.已知,在△ABC 中,DE BC∥,求证:△ADEABC∽△例 2.在△ABC 中,D、E 分别是 AB、AC 延长线上的点,且DE BC∥,试说明△ABC 与△ADE 相似例 3.如图,Rt ABC△中,∠ACB=90°,CDAB⊥于 D,请你找出图中相似的三角形,并说明理由。例 4.如图,△ABC 和△DEF 均为等边三角形,点 D、E 分别在边 AB、BC 上,请找出图中相似的三角形,并说明理由。二、利用 SSS 判定三角形相似例 1 . △ ABC 的 边 AB , BC , AC 的 长 度 分 别 为 4.2cm , 3.6cm , 3cm ; △ A’B’C’ 的 边A’B’,B’C’,A’C’的长度分别为 2.1cm,1.8cm,1.5cm,试推断△ABC 与△A’B’C’是否相似?例 2.如图,每个小正方形的边长为 1,推断△ABC 与△A’B’C’是否相似?例 3.如图,每个小正方形的边长为 1,推断△ABC 与△A’B’C’是否相似?例 4.如图,已知,求证:∠BAD=CAE∠三、利用 SAS 判定三角形相似例 1.已知△∽△,且,分别是和的中点,求证:△∽△例 2 . 已 知 △∽ △且,, 求 证 : △∽ △例 3 . 已 知 正 方 形 ABCD 中 , 点 F 为 CD 的 中 点 , 点 E 为 BC 的 四 等 分 点 , 求 证 :△CEFDFA∽△例 4.在△ABC 中,BEAC⊥,CDAB⊥,求证:△ADEABC∽△四、利用 HL 判定三角形相似例 1.已知∠C=C’=90°∠,且求证:△ABCA’B’C’∽△例 2.在 Rt ABC△和 Rt A’B’C’△中,∠C=C’=90°∠,依据下列各组条件判定这两个三角形是否相似,并说明理由。(1)∠A=35°,∠B=55°(2)AC=4,BC=5,A’C’=8,B’C’=10(3)AB=5,BC=4,A’C’=6,B’C’=8例 3.已知 Rt ABC△和 Rt A’B’C’△中,∠C=C’=90°∠,CD 和 C’D’分别是两个三角形斜边上的高,且 CD:C’D’=AC:A’C’,证明:△ABCA’B’C’∽△例 4.如图,已知∠ABC=CDB=90°∠,AC=a,BC=b,当 BD 与 a,b 之间满足怎样的关系时,△ABCBCD∽△?