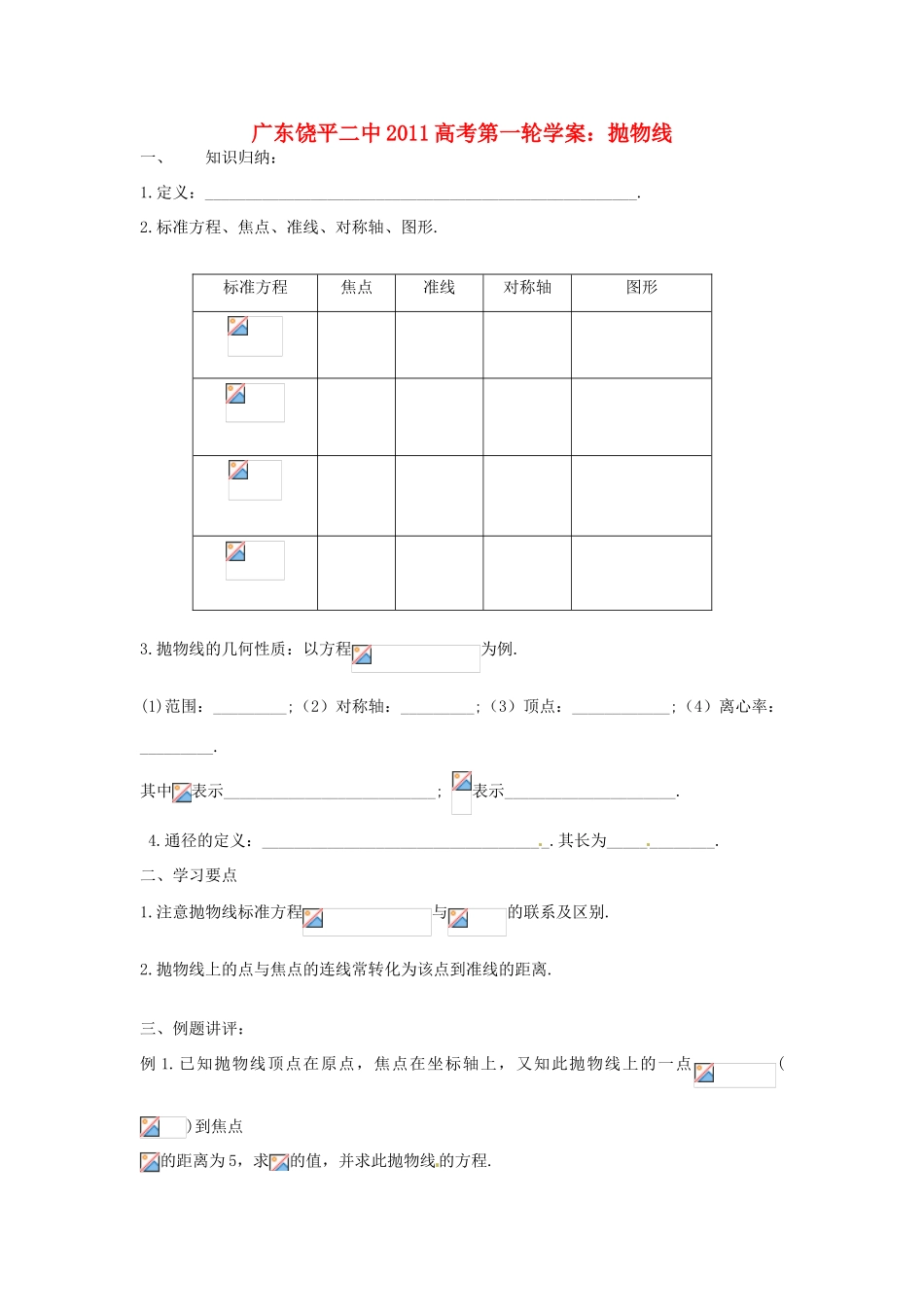
广东饶平二中 2011 高考第一轮学案:抛物线一、知识归纳:1.定义:_____________________________________________________.2.标准方程、焦点、准线、对称轴、图形.标准方程焦点准线对称轴图形3.抛物线的几何性质:以方程为例.(1)范围:_________;(2)对称轴:_________;(3)顶点:____________;(4)离心率:_________.其中表示__________________________; 表示_____________________. 4.通径的定义:___________________________________.其长为_____________.二、学习要点1.注意抛物线标准方程与的联系及区别.2.抛物线上的点与焦点的连线常转化为该点到准线的距离.三、例题讲评: 例 1.已知抛物线顶点在原点,焦点在坐标轴上,又知此抛物线上的一点()到焦点的距离为 5,求的值,并求此抛物线的方程.例 2:(1) 抛物线的准线是, 则的值为_______________.(2) 抛物线关于直线对称的曲线的焦点坐标为______________.(3) 是抛物线上一点,是抛物线的焦点,以为始边、为终边的角,则的值为______________.例 3. (1)抛物线上的点到直线距离的最小值是:A. B. C. D.(2)已知抛物线上存在关于直线对称的相 异两点 A、B,则|等于:A.3 B.4 C.3 D.4(3)对于顶点在原点的抛物线,给出下列条件:① 焦点在 y 轴上;②焦点在 x 轴上;③抛物线上横坐标为 1 的点到焦点的距离等于 6;④ 抛物线的通径的长为 5;⑤由原点向过焦点的某条直线作垂线,垂足坐标为(2,1)。能使这抛物线方程为 y2=10x 的条件是 .(要求填写合适条件的序号)四、练习题(一)选择题1.抛物线的焦点坐标是A. B. C. D.2.已知点 P 在抛物线上,那么点 P 到点的距离与点 P 到抛物线焦点距离之和取得最小值时,点 P 的坐标为:A. B. C. D. 3.已知点 P 是抛物线上的一个动点,则点 P 到点( 0,2)的距离与 P 到该抛物线准线的距离之和的最小值为:A. B. C. D.4.设为抛物线的焦点,为该抛物线上三点,若,则A.9 B.6 C.4 D.35.抛物线的焦点为,准线为 ,经过且斜率为的直线与抛物线在轴上方的部分相交于点,,垂足为,则的面积是:A. B. C.D.6.已知椭圆的中心在原点,离心率,且它的一个焦点与抛物线的焦点重合,则此椭圆方程为A.B.C.D.7.双曲线的一条渐近线与抛物线 y=x +1 只有一个公共点,则双曲线的离心率为A. B. 5 C. D.8.设抛物线=2x 的焦点为 F,过点 M(,0)的直线与抛物线相交于 A...