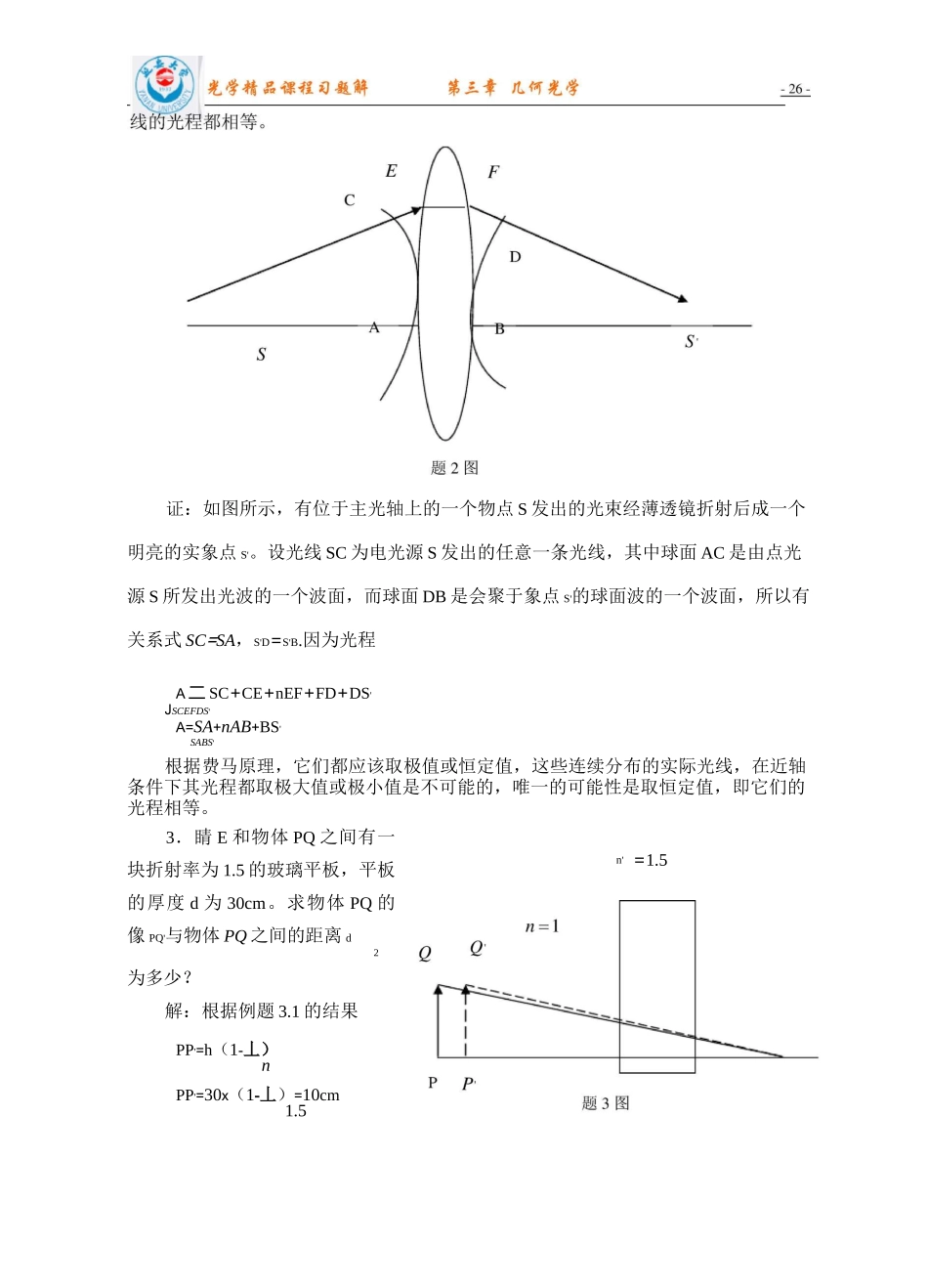
第三章几何光学1.证明反射定律符合费马原理证明:设界面两边分布着两种均匀介质,折射率为 n 和 n(如图所示)。光线通过 12在 ox 轴线上找到它的垂足点 C"点,.由于 AC>AC'',BC'>BC',故光线 AC'B 所对应的光程总是大于光线 AC''B 所对应的光程而非极小值,这就违背了费马原理。故入射面和反射面在同一平面内。(2)在图中建立坐 xoy 标系,则指定点 A,B 的坐标分别为(x,y)和(x,y),反射点1122C 的坐标为(x,0)所以 ACB 光线所对应的光程为:A=n"(x-xi)2+y2px-x2)2+y2]根据费马原理,它应取极小值,所以有dAn(x 一 x)n(x 一 x)=―; —— 1 1—12=dxv;(x—x)2+y2(x—x)2+y21122即:i=i12=n(sini—sini)=0112第一介质中指定的 A 点后到达同一介质中指定的 B 点。2.根据费马原理可以导出在近轴光线条件下,从物点发出并会聚到像点的所有光证:如图所示,有位于主光轴上的一个物点 S 发出的光束经薄透镜折射后成一个明亮的实象点 S'。设光线 SC 为电光源 S 发出的任意一条光线,其中球面 AC 是由点光源 S 所发出光波的一个波面,而球面 DB 是会聚于象点 S'的球面波的一个波面,所以有关系式 SC=SA,S'D=S'B.因为光程A 二 SC+CE+nEF+FD+DS'JSCEFDS'A=SA+nAB+BS'SABS'根据费马原理,它们都应该取极值或恒定值,这些连续分布的实际光线,在近轴条件下其光程都取极大值或极小值是不可能的,唯一的可能性是取恒定值,即它们的光程相等。3.睛 E 和物体 PQ 之间有一块折射率为 1.5 的玻璃平板,平板的厚度 d 为 30cm。求物体 PQ 的像 PQ'与物体 PQ 之间的距离 d2为多少?解:根据例题 3.1 的结果PP'=h(1-丄)nPP'=30x(1-丄)=10cm1.5=1.5n'最小偏向角;(2)此时的入射角;(3)能使光线从 A 角两侧透过棱镜的最小入射角。解:(1)等腰棱镜的折射率可以表示为sinAsm2其中 9o为最小偏向角,可以由上式解出最小偏向角2)偏向角为最小时,入射角可以表示为.9+A46o16'+6ooi==122从棱镜向外透射的最大入射角为 sini'=丄,i'=sin-1丄=38.68o2n21.6i=A-i'=60o一 38.68o=21o19'22又根据折射定律sini11=—sinin2所以 i=sin-1(sin21o19')=35o34'15•一种恒偏向棱镜,它相当于两个 30。-600-900棱镜与一个 45o-45o-900棱镜按图示方式组合在一起,白光沿 i 方向入射,我们旋转这个棱镜来改变 9,从而使任1意一种波长的光可以依次循着图示的路径传播,出射光线为 r。求证:如果 sin9=、,12...