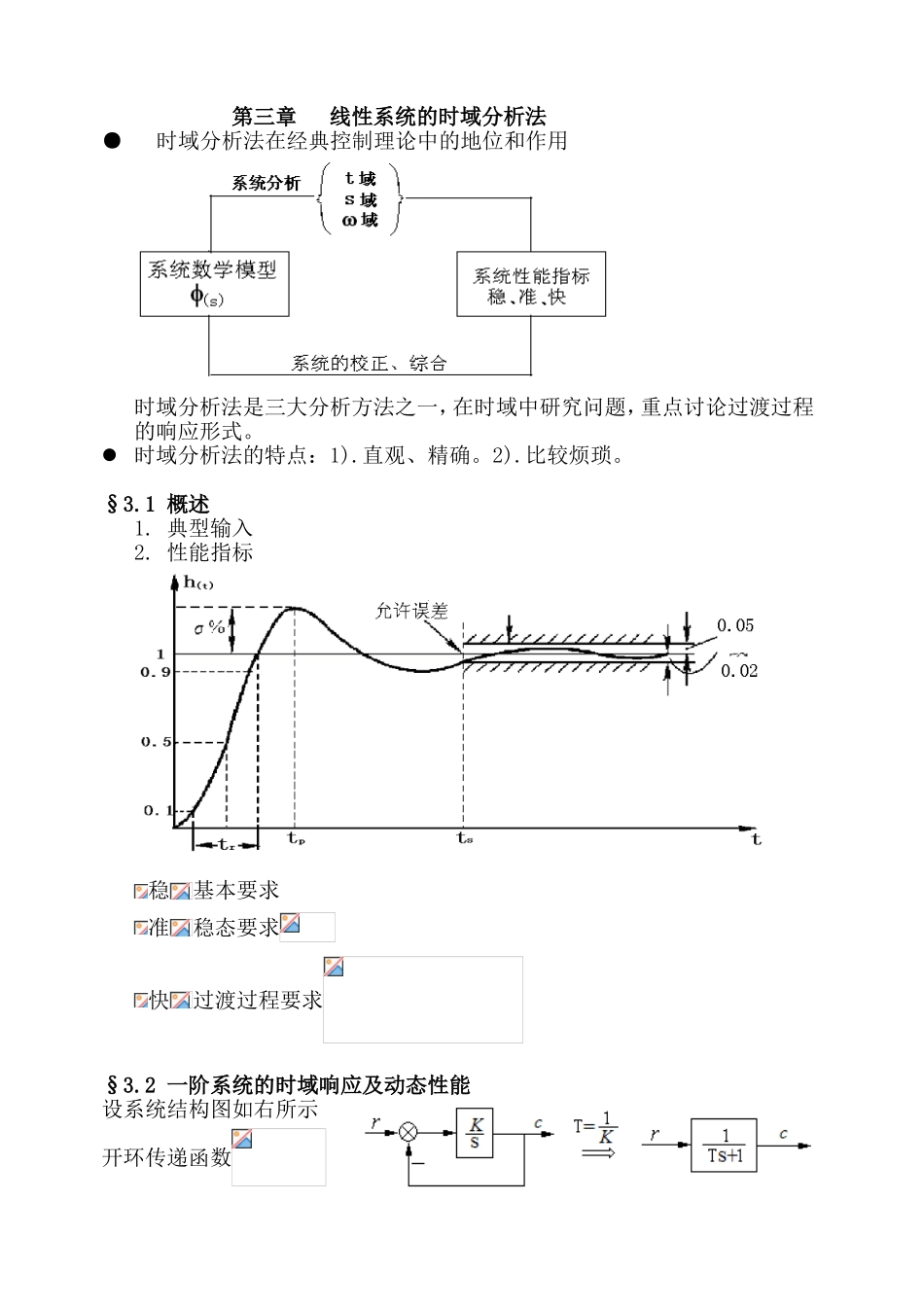
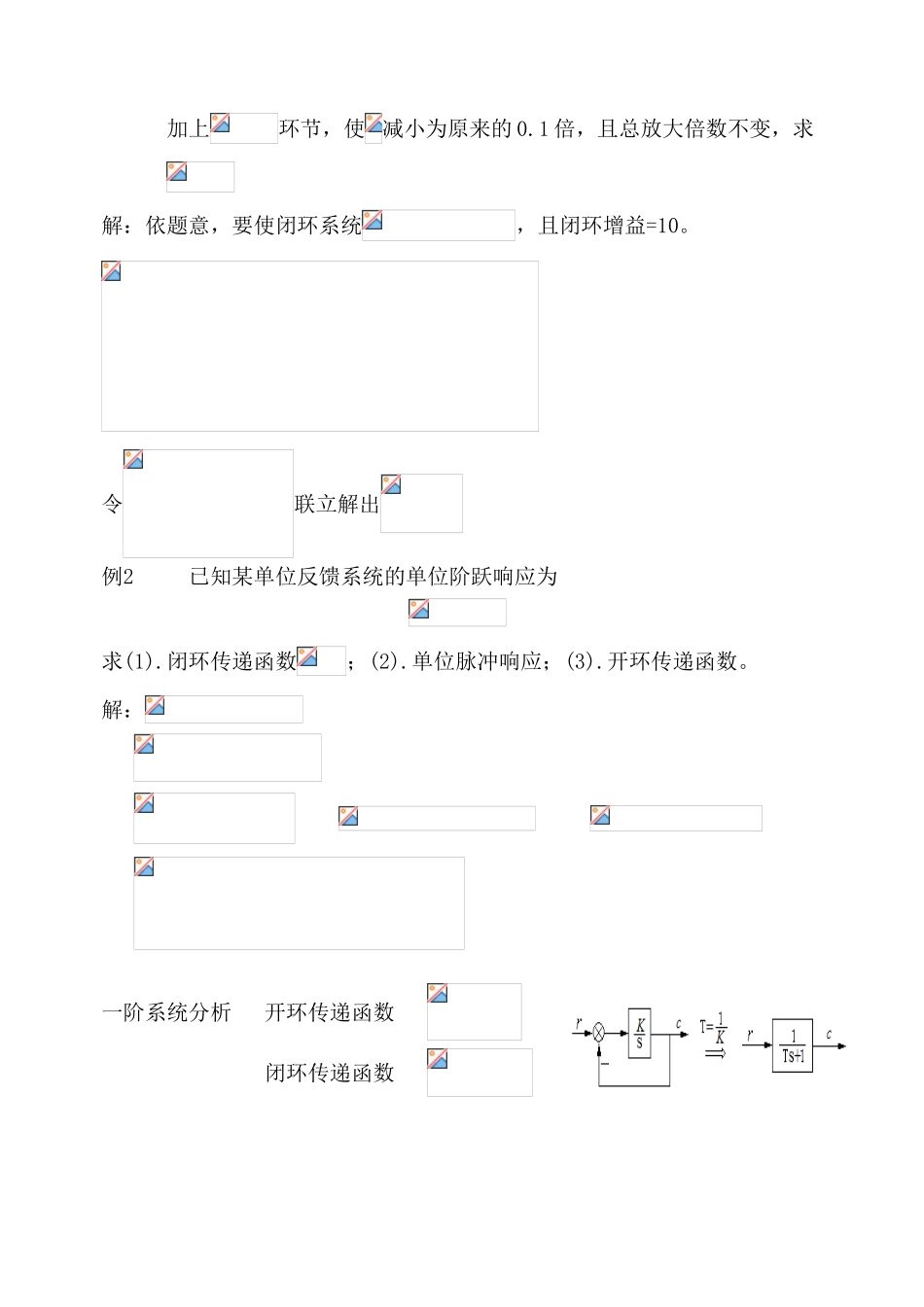
第三章线性系统的时域分析法●时域分析法在经典控制理论中的地位和作用时域分析法是三大分析方法之一,在时域中研究问题,重点讨论过渡过程的响应形式。时域分析法的特点:1).直观、精确。2).比较烦琐。§3.1概述1.典型输入2.性能指标稳基本要求准稳态要求快过渡过程要求§3.2一阶系统的时域响应及动态性能设系统结构图如右所示开环传递函数闭环传递函数依特点及定义有:一阶系统特征根分布与时域响应的关系:例1已知系统结构图如右其中:加上环节,使减小为原来的0.1倍,且总放大倍数不变,求解:依题意,要使闭环系统,且闭环增益=10。令联立解出例2已知某单位反馈系统的单位阶跃响应为求(1).闭环传递函数;(2).单位脉冲响应;(3).开环传递函数。解:一阶系统分析开环传递函数闭环传递函数●线性系统重要特性:系统对输入信号的响应,等于系统对该信号响应的§3.3二阶系统的时间响应及动态性能1.二阶系统标准形式及分类1)二阶系统典型结构及标准形式:典型结构如右=标准形式:2)二阶系统分类:负阻尼系统零阻尼系统欠阻尼系统临阻尼系统过阻尼系统2.欠阻尼二阶系统分析:⑴二阶欠阻尼系统极点的两种表示:直角坐标表示:“极”坐标表示:⑵二阶欠阻尼系统单位阶跃响应(3)指标计算:由得:即:依定义,应有)代入式:由(1)依定义忽略正弦因子影响,以包括线进入误差带的时刻为有:(3)极点分布与响应间关系例系统结构图如右,试求1)当时系统的动态性能;2)使系统阻尼比的值;3)当时系统的动态性能。解:当时:%=16.3%%=5%例2某典型欠阻尼二阶系统要求试确定系统极点的允许范围解:要求等价为:例3系统如下图示时的响应为求解:依题可知系统极点分布:3.过阻尼二阶系统性能估算:◆◆找出与之间的关系:比较:求阶跃响应:求表达式:依定义:解:)过阻尼二阶系统求思路:缺例题:例:注:1)当时,欠阻尼二阶系统—-近似用一阶系统代替2)过阻尼二阶系统零极点分布与动态性能之间的关系i.极点对影响较大――主导极点ii.与值、值有关()3)系统相当于两个惯性环节串联时的特性欠阻尼二阶系统动态性能计算复习:⑴极点的表示方法:⑵动态性能计算公式:⑶变化时动态性能的变化规律举例:系统如右图示,求分别取值为1500,200,13.5时的动态性能:解:开环传递函数开环增益150086.20.03752%0.20.004620031.60.1213%0.20.034513.58.2201.450.5111响应曲线见右下图。3单位斜坡响应与讨论:误差传递函数:(计算列表见上页表)结论:1.系统的动态性能,稳态性能均与系统结构参数()有关2.性能之间对参数的要求有时是有矛盾的必须折中,使各方面要求满足,若兼顾不到,则需校正三改善二阶系统动态性能的方法系统(如火炮系统)存在超调的原因1.比例加微分控制——提前控制改善系统性能的原理(定性分析)见下页图以说明之。2.测速反馈控制——增加阻尼(6)二阶系统性能的改善带闭环零点的欠阻尼二阶系统动态性能计算:如右系统:式中:响应:其中:指标计算:开环增益K对系统性能的影响如右系统:开环传函:开环增益:闭环传函:特征根:特征参数:动态指标:误差传函:稳态误差:*注时(讲原理)改善二阶系统动态性能的方法举例原系统(a)测速反馈(b)比例加微分(c)问题讨论:1开环增益会影响系统的性能指标改变指标的原因:开环增益闭环增益变化→特征多项式系数变化→特征根变化→变化→性能变化开环增益变化对性能的改善是有限的,指标对的要求往往是矛盾的只能采取折中方案,兼顾不同的要求。“快”与“准”两项指标相矛盾2.闭环增益不改变系统性能指标,只改变输出的比例尺度3.系统的性能不仅取决于闭环极点,而且与闭零点有关。前者决定响应的模态,后者决定模态的加权系数。4.不同输入下稳态误差分析⒌比例—微分控制的原理——提前控制(图示)⒍测速反馈改善性能的原理——增加阻尼(从结构图解释)⒎两种方案比例—微分测速反馈1)对噪声敏感;信号弱,需放大;有滤波作用,信号强,不需放大;2)较简单,成本低;复杂,成本高;3)不改变开环增益,不改变;改变开环增益,4)引入一个闭零点()。不引入闭零点。⒏附加开环零点的作用:——原系统与测速反馈系统相比较原系...