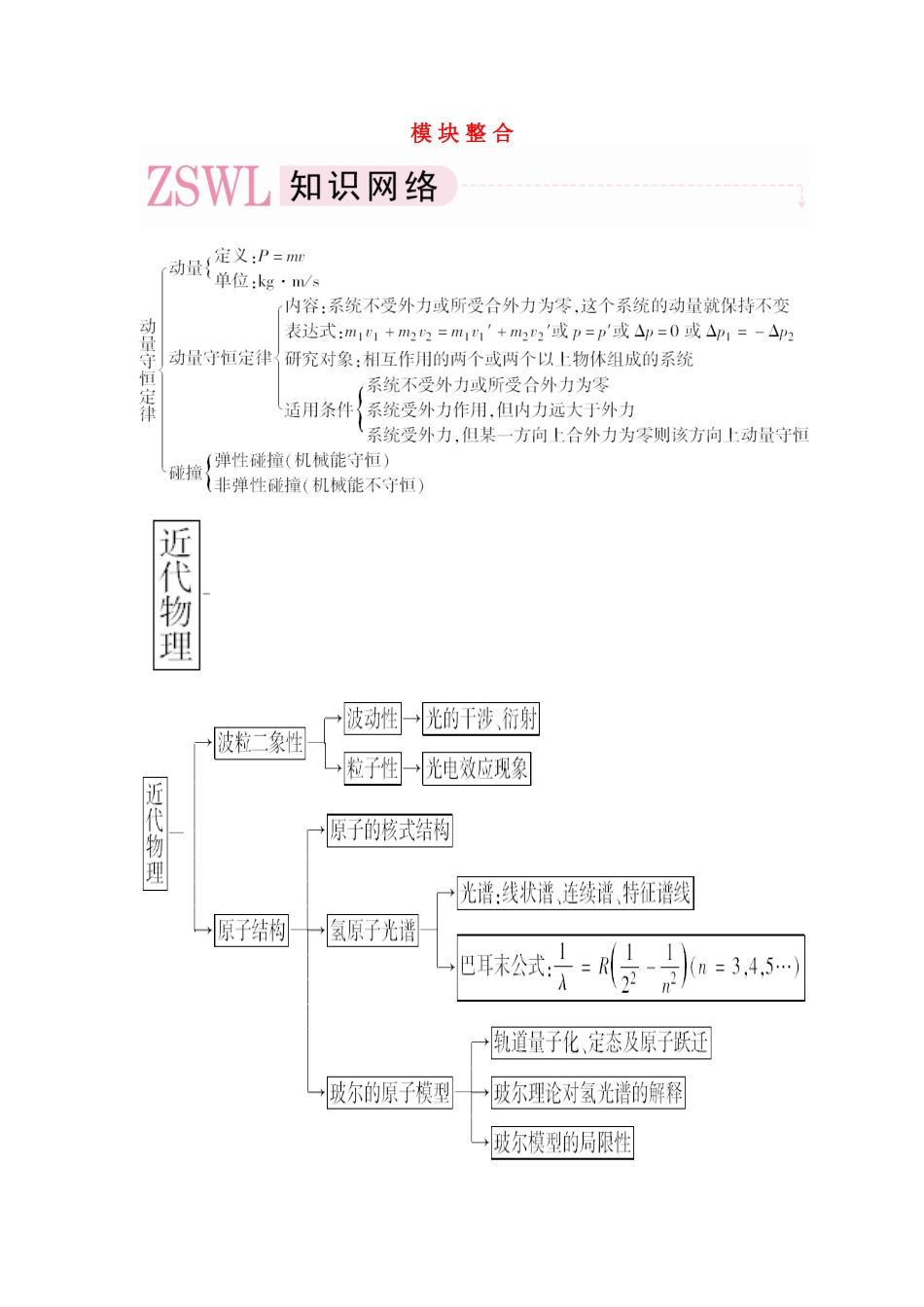
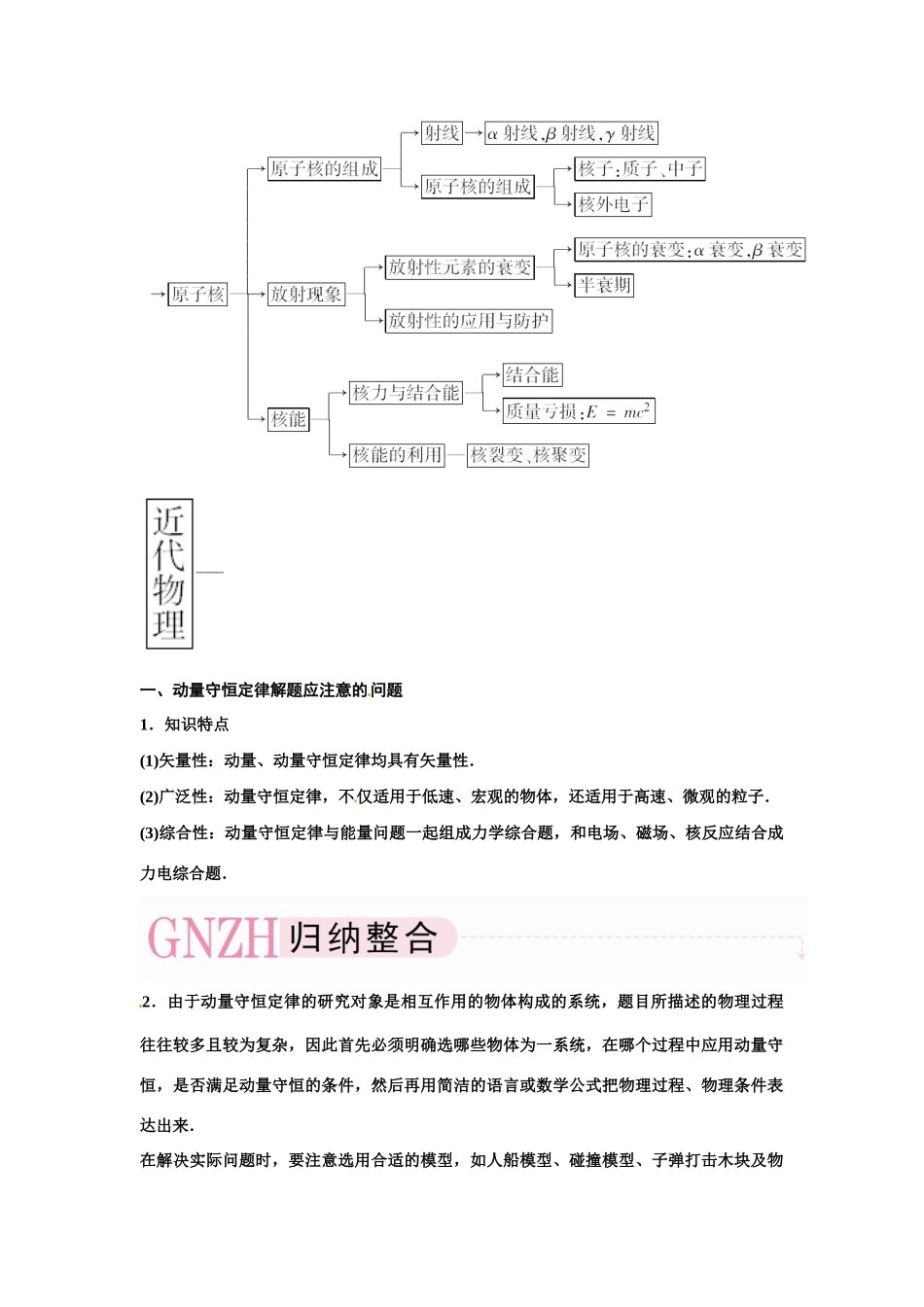
模 块 整 合一、动量守恒定律解题应注意的问题1.知识特点(1)矢量性:动量、动量守恒定律均具有矢量性.(2)广泛性:动量守恒定律,不仅适用于低速、宏观的物体,还适用于高速、微观的粒子.(3)综合性:动量守恒定律与能量问题一起组成力学综合题,和电场、磁场、核反应结合成力电综合题.2.由于动量守恒定律的研究对象是相互作用的物体构成的系统,题目所描述的物理过程往往较多且较为复杂,因此首先必须明确选哪些物体为一系统,在哪个过程中应用动量守恒,是否满足动量守恒的条件,然后再用简洁的语言或数学公式把物理过程、物理条件表达出来.在解决实际问题时,要注意选用合适的模型,如人船模型、碰撞模型、子弹打击木块及物块在木板上滑行的模型,提高综合分析问题的能力和对实际问题抽象简化的能力.3.碰撞问题是应用动量守恒定律的重头戏,既有定量计算的难题,也有定性分析判断的活题.要牢固掌握两球碰撞后可 能状态判断的依据,即:(1)碰撞前后应符合系统动量守恒.(2)碰撞后的总动能应不大于碰撞前的总动能.(3)所给碰撞后两球的位置和状态应符合实际.如:后球不应超越前球;两球动量的变化(含方向)应符合作用规律等.对导出式 Ek= 要能够熟练地应用.[例 1] 如图所示,一质量为 m1 的小物块 A 从距水平面高为 h 的光滑弯曲坡道顶端由静止滑下,然后进入水平面上的滑道(它与弯曲坡道相切).为使 A 制动,将轻质弹簧的一端固定在水平滑道左端的墙壁上 M 处,另一端与质量为 m2 的挡板 B 相连,整个弹簧处于水平,当弹簧处于原长时,B 恰好位于滑道上的 O 点,已知 A 与 B 碰撞时间极短,碰后一起共同压缩弹簧(但不粘连),最大压缩量为 d,在水平面的 OM 段 A、B 与地面间的动摩擦因数均为 μ,ON 段光滑,重力加速度为 g,弹簧处于原长时弹性势能为零.求:(1)物块 A 在与挡板 B 碰撞前的瞬时速率 v;(2)弹簧最大压缩量为 d 时的弹性势能 Ep;(3)若物体 A 能反弹回坡道上,求反弹的最大高度 H.[解析] (1)A 下降过程中只有重力做功,机械能守恒(2)A、B 碰撞过程中,动量守恒,设碰后速度为 v1m1v=(m1+m2)v1③A、B 压缩弹簧过程中,由功能关系μ(m1+m2)gd+Ep= (m1+m2) ④解③④可得:Ep= -μ(m1+m2)gd.⑤A 离开 B 沿斜面上升,机械能守恒二、近代物理学问题的处理1.实验法:研究物理学的重要手段,近代物理中的很多物理规律都是通过实验获取的.2.假设法:通...