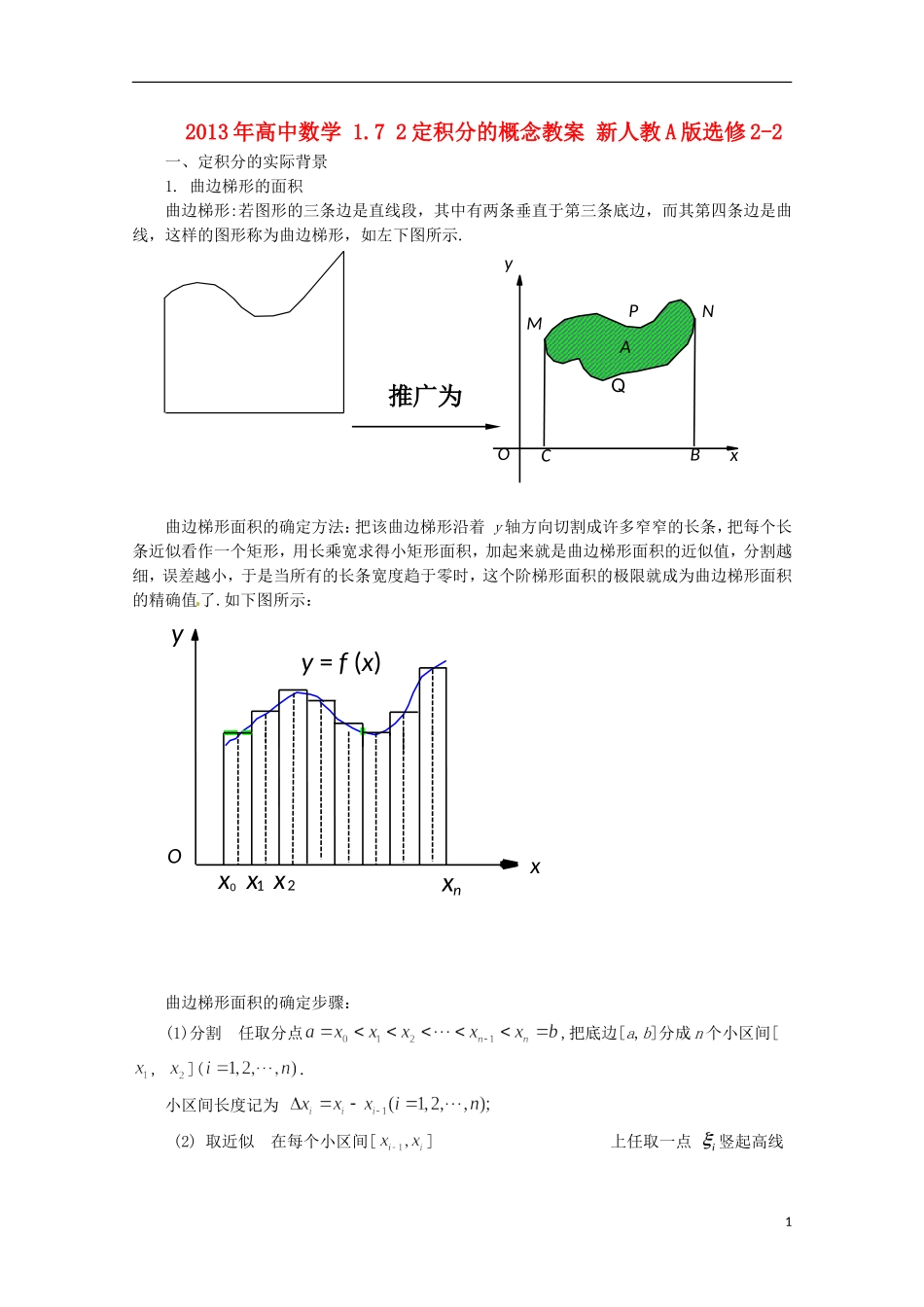
2013 年高中数学 1.7 2 定积分的概念教案 新人教 A 版选修 2-2一、定积分的实际背景1. 曲边梯形的面积曲边梯形:若图形的三条边是直线段,其中有两条垂直于第三条底边,而其第四条边是曲线,这样的图形称为曲边梯形,如左下图所示.曲边梯形面积的确定方法:把该曲边梯形沿着 y 轴方向切割成许多窄窄的长条,把每个长条近似看作一个矩形,用长乘宽求得小矩形面积,加起来就是曲边梯形面积的近似值,分割越细,误差越小,于是当所有的长条宽度趋于零时,这个阶梯形面积的极限就成为曲边梯形面积的精确值了.如下图所示: 曲边梯形面积的确定步骤:(1)分割 任取分点,把底边[a,b]分成 n 个小区间[, ](. 小区间长度记为 (2) 取近似 在每个小区间[]上任取一点 竖起高线yOMPQNBxCAA0x1x2xxn Oxy y = f (x)1推广为,则得小长条面积的近似值为 (); (3) 求和 把 n 个小矩形面积相加(即阶梯形面积)就得到曲边梯形面积 A 的近似值;(4)取极限 令小区间长度的最大值 趋于零,则和式 的极限就是曲边梯形面积 A 的精确值,即2.变速直线运动的路程 设某物体作直线运动,已知速度是时间间隔[]上的连续函数,且≥0,要计算这段时间内所走的路程. 解决这个问题的思路和步骤与上例类似:(1)分割 任取分点,把[]分成 个小段,每小段长为 (); (2)取近似 把每小段[ ]上的运动视为匀速,任取时刻,作乘积,显然这小段时间所走路程 可近似表示为 ();(3)求和 把 n 个小段时间上的路程相加,就得到总路程 s 的近似值,即 ;(4) 取 极 限 当 时 , 上 述 总 和 的 极 限 就 是的 精 确 值 , 即.二、定积分的概念 定义 设函数在上有定义,任取分点,分为 n 个小区间.记 , 再在每个小区间上任取一点 ,作乘积 的和式:如果时,上述极限存在(即,这个极限值与 的分割及点的取法均无关),则称此极限值为函数在区间上的定积分,记为2其中称为被积函数,为被积式, 为积分变量,为积分区间,分别称为积分下限和上限.定积分定义的说明:(1)定积分表示一个数,它只取决于被积函数与积分上、下限,而与积分变量采用什么字母无关,例如: .一般地,. (2)定义中要求积分限 ,我们补充如下规定:当 时,,当 时, .(3)定积分的存在性:当 在 上连续或只有有限个第一类间断点时, 在上的定积分存在(也称可积).三、定积分的几何意义如 果 , 则, 此 时表 示 由 曲 线,,xa xb ...