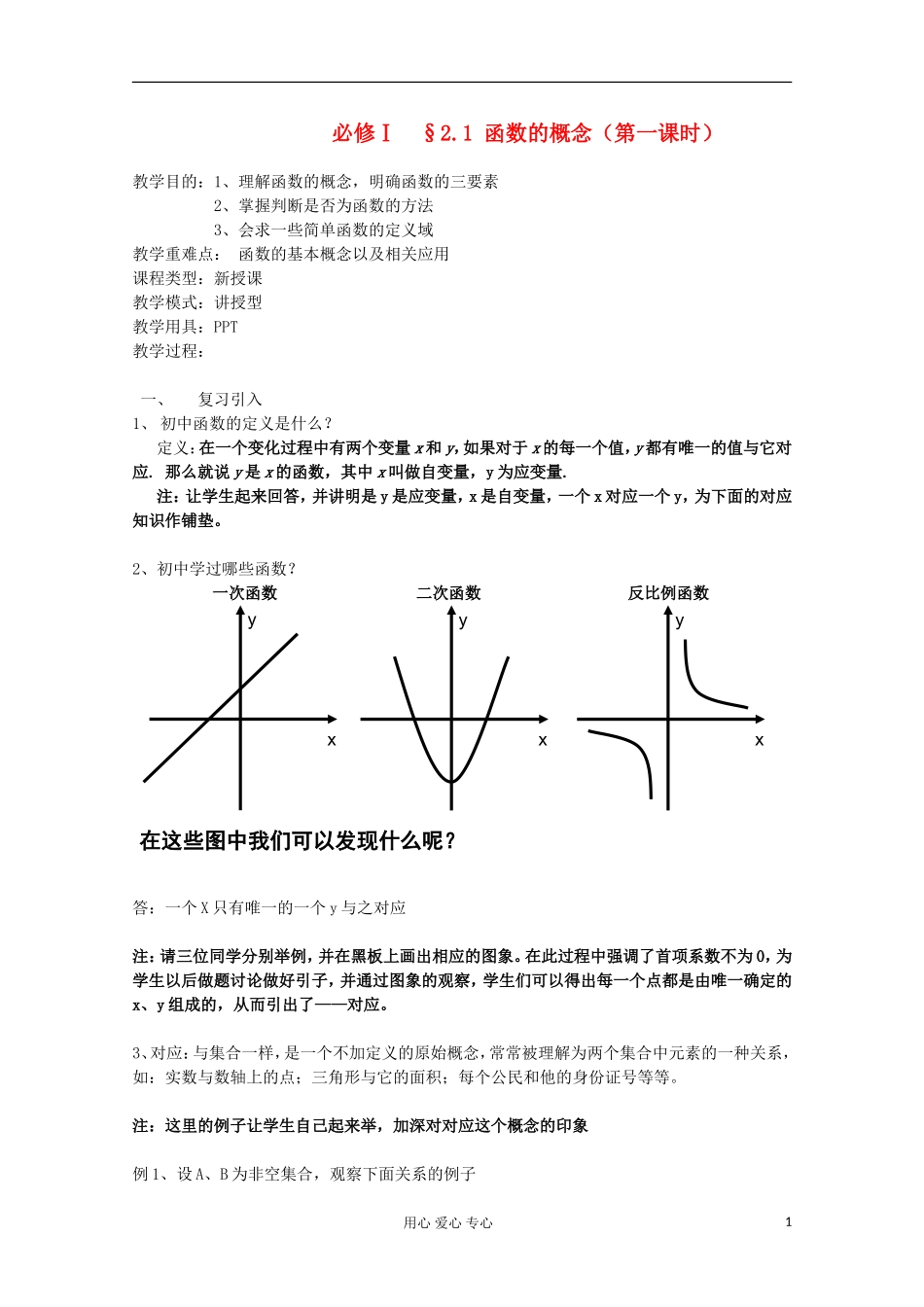
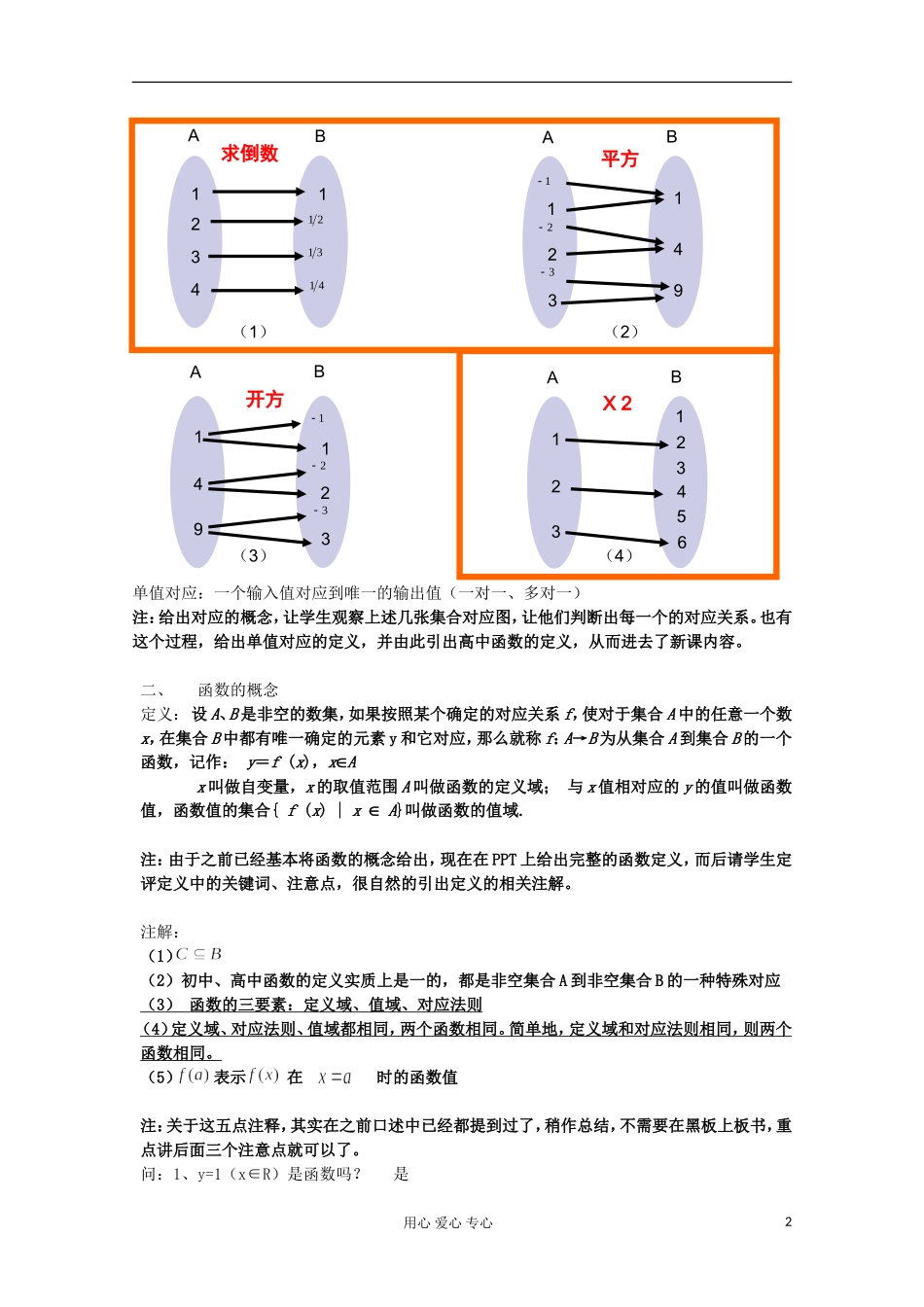
必修Ⅰ §2.1 函数的概念(第一课时)教学目的:1、理解函数的概念,明确函数的三要素 2、掌握判断是否为函数的方法 3、会求一些简单函数的定义域教学重难点: 函数的基本概念以及相关应用课程类型:新授课教学模式:讲授型教学用具:PPT教学过程:一、复习引入1、 初中函数的定义是什么?定义:在一个变化过程中有两个变量 x 和 y,如果对于 x 的每一个值,y 都有唯一的值与它对应. 那么就说 y 是 x 的函数,其中 x 叫做自变量,y 为应变量. 注:让学生起来回答,并讲明是 y 是应变量,x 是自变量,一个 x 对应一个 y,为下面的对应知识作铺垫。2、初中学过哪些函数?一次函数 二次函数 反比例函数答:一个 X 只有唯一的一个 y 与之对应注:请三位同学分别举例,并在黑板上画出相应的图象。在此过程中强调了首项系数不为 0,为学生以后做题讨论做好引子,并通过图象的观察,学生们可以得出每一个点都是由唯一确定的x、y 组成的,从而引出了——对应。3、对应:与集合一样,是一个不加定义的原始概念,常常被理解为两个集合中元素的一种关系,如:实数与数轴上的点;三角形与它的面积;每个公民和他的身份证号等等。注:这里的例子让学生自己起来举,加深对对应这个概念的印象例 1、设 A、B 为非空集合,观察下面关系的例子用心 爱心 专心xyyxyx在这些图中我们可以发现什么呢?1单值对应:一个输入值对应到唯一的输出值(一对一、多对一)注:给出对应的概念,让学生观察上述几张集合对应图,让他们判断出每一个的对应关系。也有这个过程,给出单值对应的定义,并由此引出高中函数的定义,从而进去了新课内容。二、函数的概念定义: 设 A、B 是非空的数集,如果按照某个确定的对应关系 f,使对于集合 A 中的任意一个数x,在集合 B 中都有唯一确定的元素 y 和它对应,那么就称 f:A→B 为从集合 A 到集合 B 的一个函数,记作: y=f (x),xÎAx 叫做自变量,x 的取值范围 A 叫做函数的定义域; 与 x 值相对应的 y 的值叫做函数值,函数值的集合{ f (x) | x Î A}叫做函数的值域.注:由于之前已经基本将函数的概念给出,现在在 PPT 上给出完整的函数定义,而后请学生定评定义中的关键词、注意点,很自然的引出定义的相关注解。注解:(1)(2)初中、高中函数的定义实质上是一的,都是非空集合 A 到非空集合 B 的一种特殊对应( 3 ) 函数的三要素:定义域、值域...