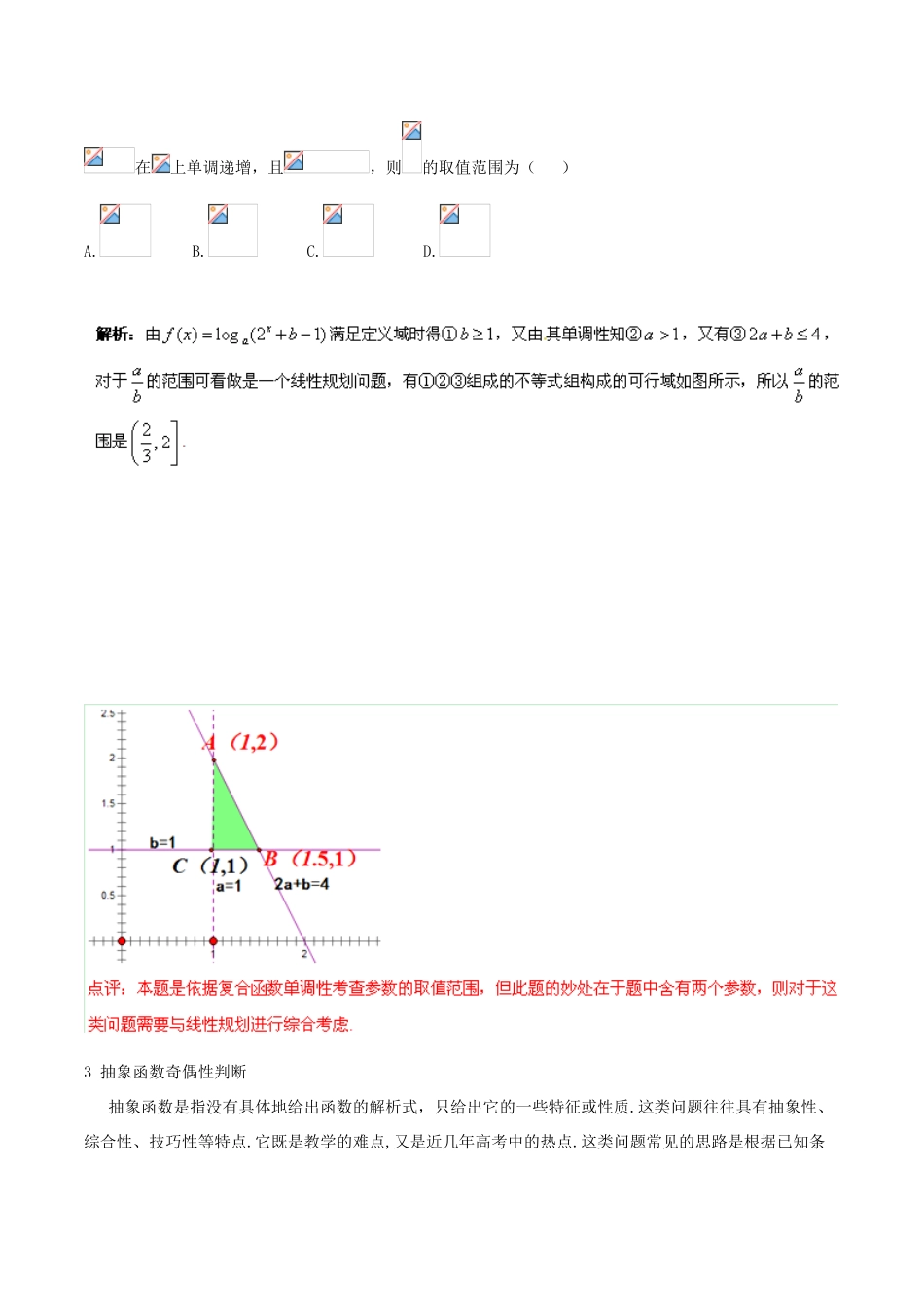
2014 年高考数学二轮复习精品资料 难点 07 函数的性质综合运用问题学案(含解析)函数性质的综合应用是高考的重点内容之一,考查的内容灵活多样,函数的奇偶性、单调性、周期性、对称性可以单独命题,也可以将它们综合在一起进行考查,很多学生在做题时不能很准确的利用好各个性质的特征进行解题,从而导致正确率很低.同时试题中往往以抽象函数为题根,来考查考生对函数性质的理解和掌握,而抽象函数就是考生的弱点之一,因而这种类型的试题,难度较大.本文就高考中常见考查题型加以总结和方法的探讨.1 函数单调性的判断 函数单调性判断的常用方法:(1)利用已知函数的单调性,即转化为已知函数的和、差或复合函数,求单调区间.(2)定义法:先求定义域,再利用单调性定义.(3)图象法:如果是以图象形式给出的,或者的图象易作出,可由图象的直观性写出它的单调区间.(4)导数法:利用导数的正负确定函数的单调区间.例 1【江苏省灌云高级中学 2013-2014 学年度高三第一学期期中考试】函数的单调递增区间为 .2 依据函数单调性求参数范围 对于含参函数在给定区间内单调递减(以递减为例)求参数范围,可以根据具体的函数单调性考虑,也可以根据函数求导考虑,然后转化成恒成立问题. 常见的利用导数的方法有:(1)最值法:先对给定函数进行求导,则原题意转化为对于一切恒成立,此时只需求出在上的最大值(是关于的表达式),再解不等式,进行得到的取值范围.(2)子区间法:先解关于的不等式,得到用参数表示的函数的单调减区间,再令,从而可以得到关于的不等式或不等式组,进而得到的取值范围.(3)参数分离法:先对给定函数进行求导,则原题意转化为对于一切恒成立,将参数分离到不等式的一边,而另一边是一个不含参数的函数,若参数分离后得到不等式,则(反之,).例 2 【 安 徽 省 毫 州 市 涡 阳 四 中 2014 届 高 三 上 学 期 第 二 次 月 考 数 学 ( 理 ) 】 已 知是上的单调递增函数,则实数的取值范围为 ( )A.(1,+∞) B.[4,8) C.(4,8) D.(1,8)例 3【安徽省合肥市 2014 届高三第一次质量检测数学(文)】已知函数且在上单调递增,且,则的取值范围为( ) A. B. C. D.3 抽象函数奇偶性判断 抽象函数是指没有具体地给出函数的解析式,只给出它的一些特征或性质.这类问题往往具有抽象性、 综合性、技巧性等特点.它既是教学的难点,又是近几年高考中的热点.这类问题常...