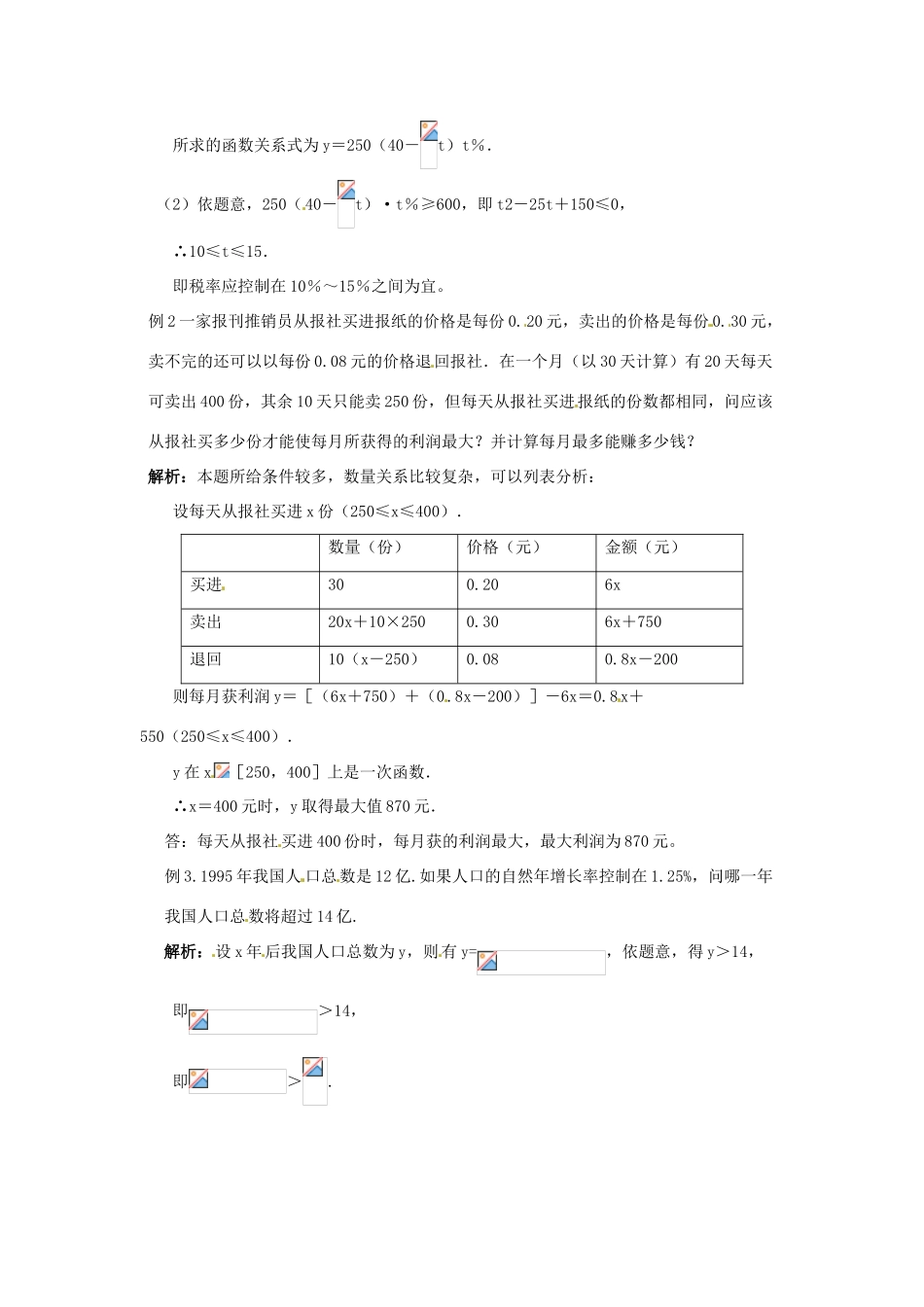
3.2 函数模型及其应用学习过程知识点一: 解决函数应用题的基本步骤:第一步:认真读题,缜密审题,确切理解题意,明确问题实际背景,然后进行科学的抽象概括,将实际问题转化成数学问题,即实际问题数学化. 第二步:运用所学的数学知识和数学方法解答函数问题,得出函数问题的解.第三步:将所得函数问题的解代入实际问题进行验证,看是否符合实际,并对实际问题作答.知识点二:解决函数应用题的流程图是: 学习结论 (1)抽象出数学模型时,除了考虑式子的本身意义外,还需注意实际问题对变量范围的限制。(2)解决函数应用题的关键是将实际问题转化成数学问题,即实际问题数学化。典型例题例 1.某地方政府为保护地方电子工业发展,决定对某一进口电子产品征收附加税.已知这种电子产品国内市场零售价为每件 250 元,每年可销售 40 万件,若政府增加附加税率为每百元收 t 元时,则每年销售量将减少t 万件. (1)将税金收入表示为征收附加税率的函数; (2)若在该项经营中每年征收附加税金不低于 600 万元,那么附加税率应控制在什么范围?解析:(1)设每年销售是 x 万件,则每年销售收入为 250x 万元,征收附加税金为 y=250x% 依题意,x=40-t. 所求的函数关系式为 y=250(40-t)t%. (2)依题意,250(40-t)·t%≥600,即 t2-25t+150≤0, ∴10≤t≤15. 即税率应控制在 10%~15%之间为宜。例 2 一家报刊推销员从报社买进报纸的价格是每份 0.20 元,卖出的价格是每份 0.30 元,卖不完的还可以以每份 0.08 元的价格退回报社.在一个月(以 30 天计算)有 20 天每天可卖出 400 份,其余 10 天只能卖 250 份,但每天从报社买进报纸的份数都相同,问应该从报社买多少份才能使每月所获得的利润最大?并计算每月最多能赚多少钱?解析:本题所给条件较多,数量关系比较复杂,可以列表分析: 设每天从报社买进 x 份(250≤x≤400).数量(份)价格(元)金额(元)买进300.206x卖出20x+10×2500.306x+750退回10(x-250)0.080.8x-200 则每月获利润 y=[(6x+750)+(0.8x-200)]-6x=0.8x+550(250≤x≤400). y 在 x[250,400]上是一次函数. ∴x=400 元时,y 取得最大值 870 元.答:每天从报社买进 400 份时,每月获的利润最大,最大利润为 870 元。例 3.1995 年我国人 口总数是 12 亿.如果人口的自然年增长率控制在 1.25%,问哪一年我国...