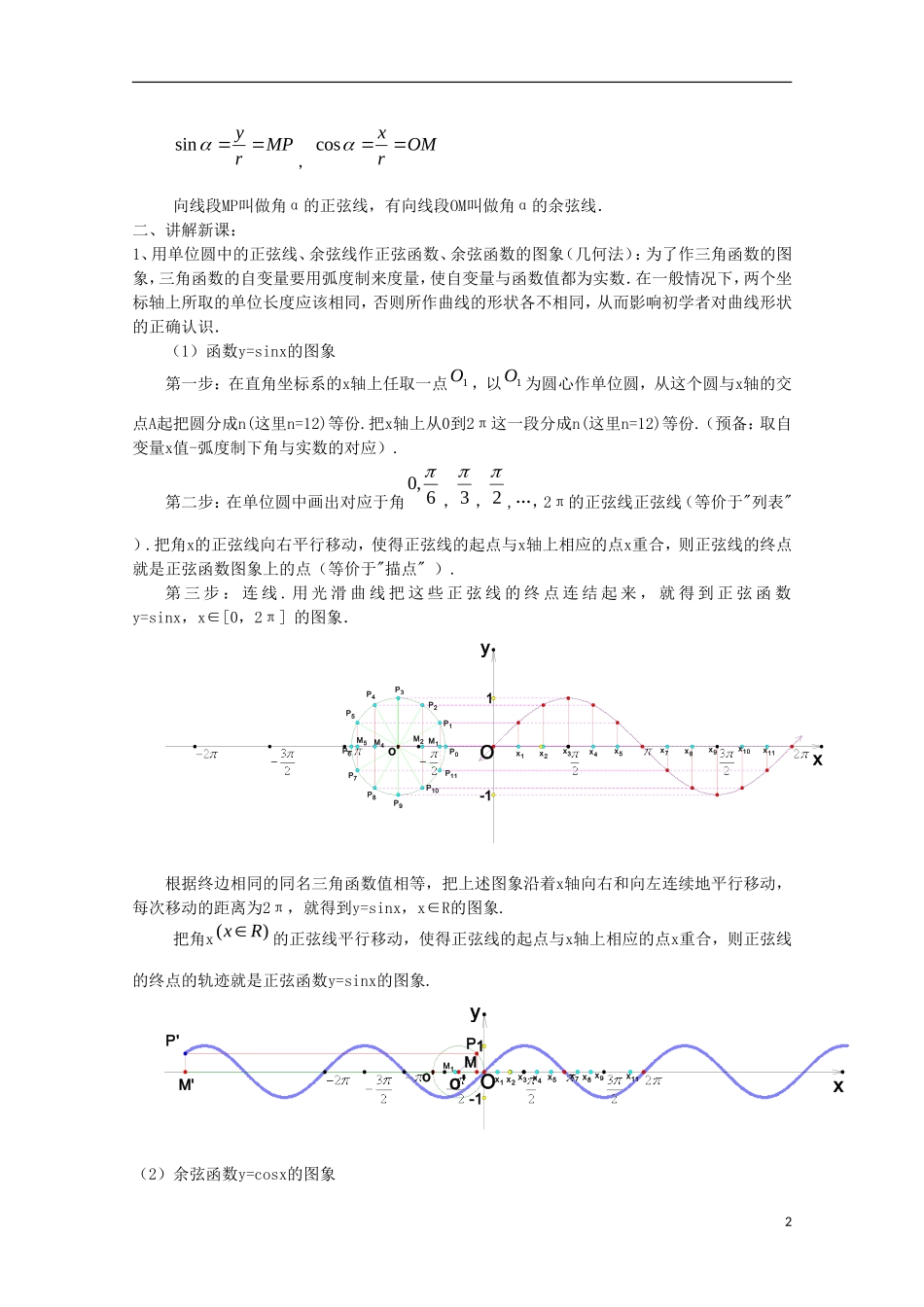
1.4.1正弦、余弦函数的图象(1)教学目的:知识目标:(1)利用单位圆中的三角函数线作出Rxxy,sin的图象,明确图象的形状;(2)根据关系)2sin(cosxx,作出Rxxy,cos的图象;(3)用"五点法"作出正弦函数、余弦函数的简图,并利用图象解决一些有关问题;能力目标:(1)理解并掌握用单位圆作正弦函数、余弦函数的图象的方法;(2)理解并掌握用"五点法"作正弦函数、余弦函数的图象的方法; 德育目标:通过作正弦函数和余弦函数图象,培养学生认真负责,一丝不苟的学习和工作精神;教学重点:用单位圆中的正弦线作正弦函数的图象; 教学难点:作余弦函数的图象,周期性; 授课类型:新授课教学模式:启发、诱导发现教学.教 具:多媒体、实物投影仪教学过程:一、复习引入:1. 弧度定义:长度等于半径长的弧所对的圆心角称为1弧度的角。2.正、余弦函数定义:设 是一个任意角,在 的终边上任取(异于原点的)一点P(x,y)ry)(x,PP与原点的距离r(02222yxyxr)则比值 ry叫做 的正弦 记作: rysin 比值 rx叫做 的余弦 记作: rxcos3.正弦线、余弦线:设任意角α的终边与单位圆相交于点P(x,y),过P作x轴的垂线,垂足为M,则有1MPry sin,OMrx cos向线段MP叫做角α的正弦线,有向线段OM叫做角α的余弦线.二、讲解新课: 1、用单位圆中的正弦线、余弦线作正弦函数、余弦函数的图象(几何法):为了作三角函数的图象,三角函数的自变量要用弧度制来度量,使自变量与函数值都为实数.在一般情况下,两个坐标轴上所取的单位长度应该相同,否则所作曲线的形状各不相同,从而影响初学者对曲线形状的正确认识.(1)函数y=sinx的图象第一步:在直角坐标系的x轴上任取一点1O ,以1O 为圆心作单位圆,从这个圆与x轴的交点A起把圆分成n(这里n=12)等份.把x轴上从0到2π这一段分成n(这里n=12)等份.(预备:取自变量x值-弧度制下角与实数的对应).第二步:在单位圆中画出对应于角6,0 ,3,2,…,2π的正弦线正弦线(等价于"列表" ).把角x的正弦线向右平行移动,使得正弦线的起点与x轴上相应的点x重合,则正弦线的终点就是正弦函数图象上的点(等价于"描点" ). 第 三 步 : 连 线 . 用 光 滑 曲 线 把 这 些 正 弦 线 的 终 点 连 结 起 来 , 就 得 到 正 弦 函 数y=sinx,x∈[0,2π] 的图象.-11x11x10x8x7x5x4x3x2x1M5M4M2 M1P11P10P9P8...