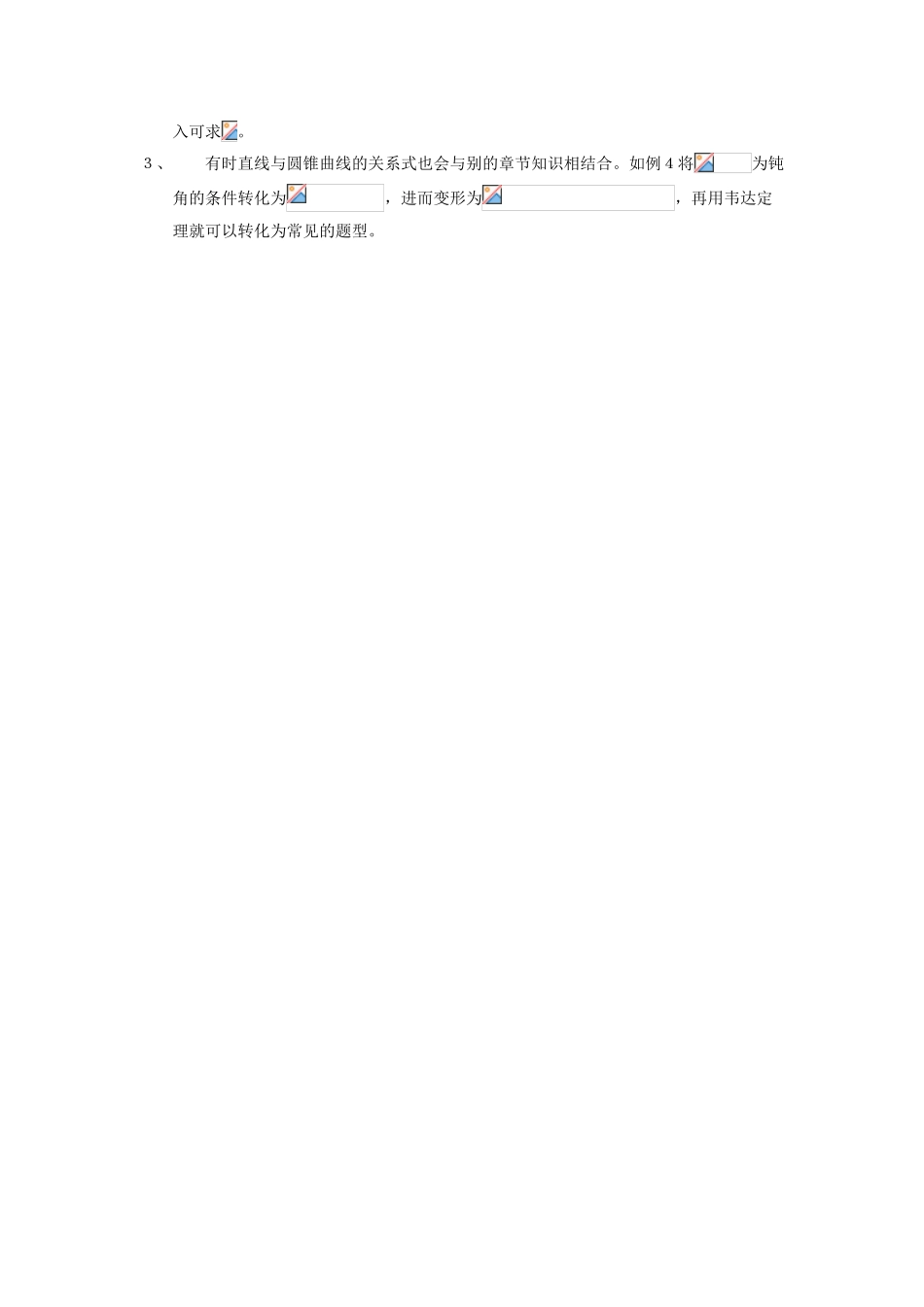
第 20 讲 直线与圆锥曲线的位置关系(2)一、复习目标1、会利用圆锥曲线的定义处理焦点弦、弦长等问题;2、能够根据圆锥曲线图形的特征判断直线与曲线的位置关系问题,进而判断直线与曲线的交点个数;3、强化运用数形结合的思想方法分析、判断,能综合运用函数、方程、不等式的知识解决相关问题.二、基础回顾1、过椭圆的左焦点 引直线交椭圆于两点,若,则此直线的方程为______________________.2、已知动点在抛物线上,且到此抛物线的准线距离为,当点到直线的距离最小时,等于( )、 、 13、已知椭圆为长轴的一个端点,弦过椭圆的中心,且,则椭圆的焦距为( ) 以上答案都不对4、B 地在 A 地的正东方向 4处,C 地 在 B 地的北偏东 30°方向 2处,河流的沿岸PQ(曲线)上任意一点到 A 的距离比到 B 的距离远 2,现要在曲线 PQ 上选一处 M 建一座码头,向 B,C 两地转运货物,经测算,从 M 到 B,M 到 C 修建公路的费用分别是万元/,2万元/,那么修建这两条公路的总费用最低是( )万元。、 、 、 、5、、若以圆锥曲线的一条经过焦点的弦为直径的圆与对应的准线有两个交点,则此圆锥曲线为( )A. 双曲线 B.椭圆 C.抛物线 D. 椭圆或双曲线推广(1)若是椭圆或抛物线呢?(2)若是双曲线,所交弦对应的圆心角是否为定值?三、例题探究例 1、已知双曲线以两条坐标轴为对称轴,且与 x2+y2=17 圆相交于 A(4,-1),若圆在点 A 的切线与双曲线的一条渐近线平行,求双曲线的方程. 例 2、已知,O为坐标原点,点满足+=6(1)点的轨迹的方程。(2)是否存在直线 过点,与轨迹交于两点,且以为直径的圆过原点?若存在,求出直线 的方程,若不存在,请说明理由。例 3、如图:,点A在y轴上,点Q在轴的正半轴上,且,在的延长线上取一点(1)当A点在y轴上移动时,求动点的轨迹C的方程(2)已知,经过为方向向量的直线 与轨迹C交于E,F两点,又点,若为钝角时,求的取值范围〔备用题〕椭圆的左、右顶点分别为,点是双曲线在第一象限内的图象上的一点,直线与椭圆分别交于点,若是的中点(1)求点的坐标。(2)能否使直线过椭圆的右焦点?若能,求出双曲线的离心率;若不能,请说明理由。四、方法点拨1、已知双曲线的渐近线,可以不分类讨论,先观察图形确定焦点在哪个轴上。如例1)2、直线与圆锥曲线的位置关系联立方程组是经常采用的手段。如例2以为直径的圆过原点就是,而,将...