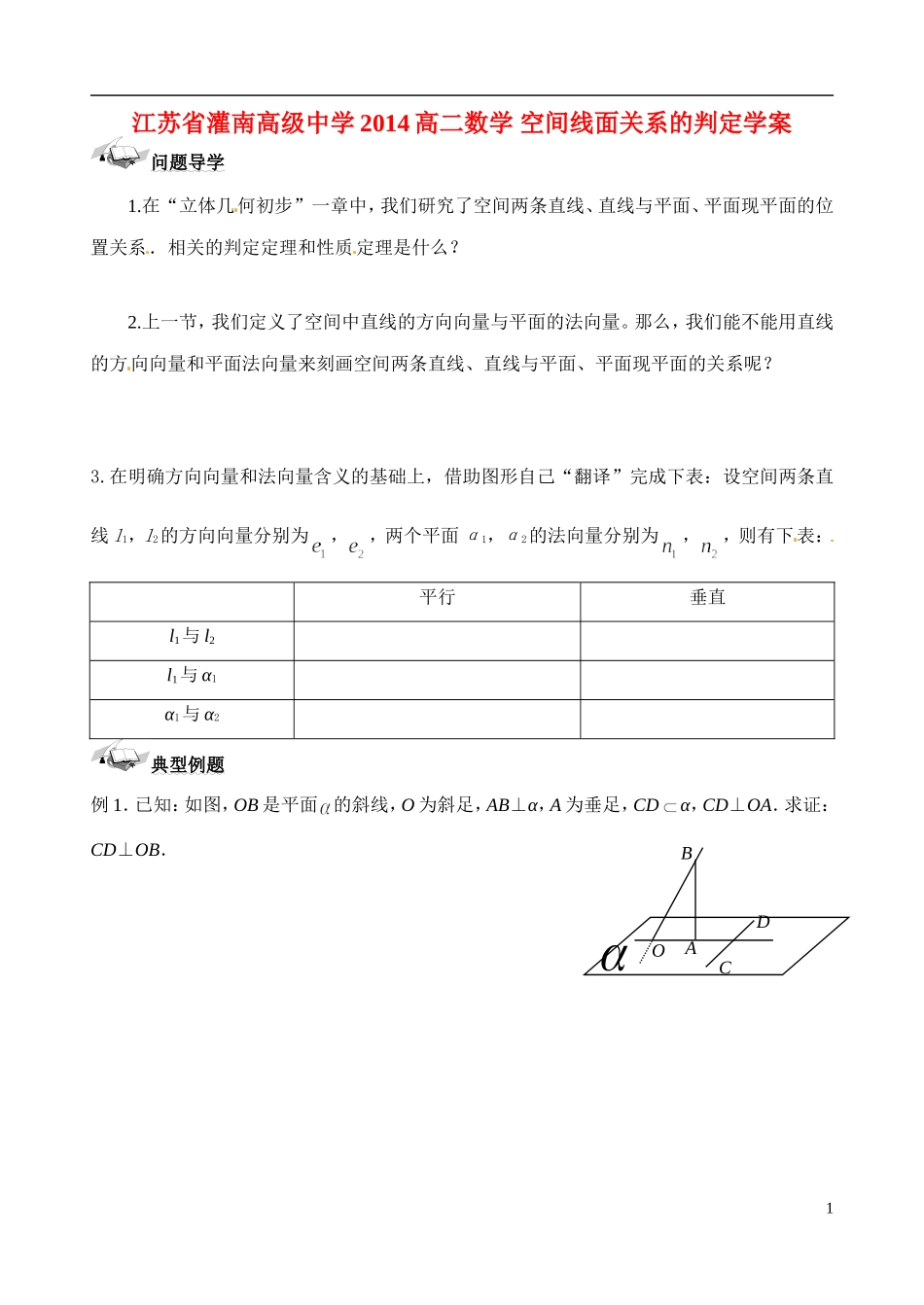
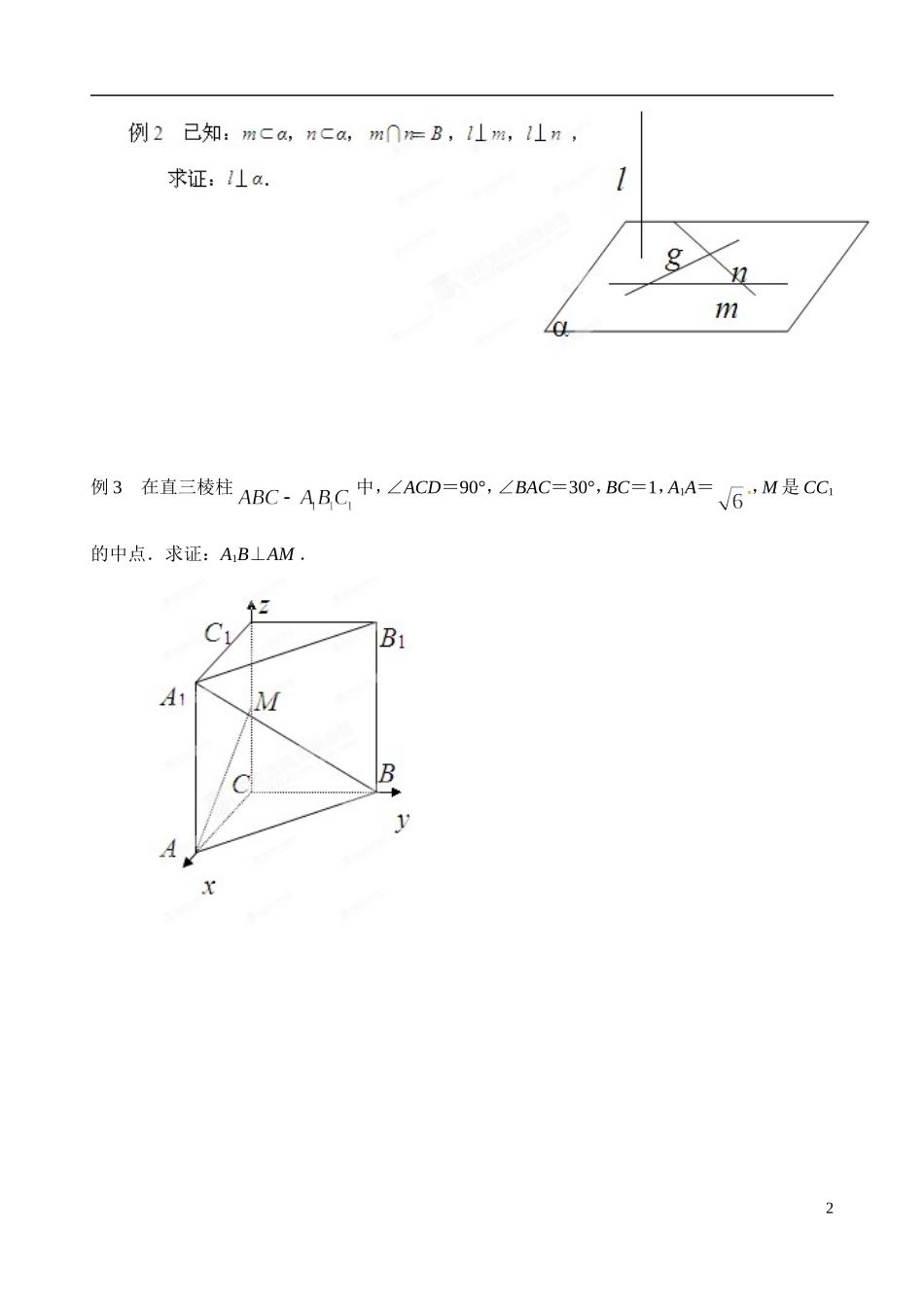
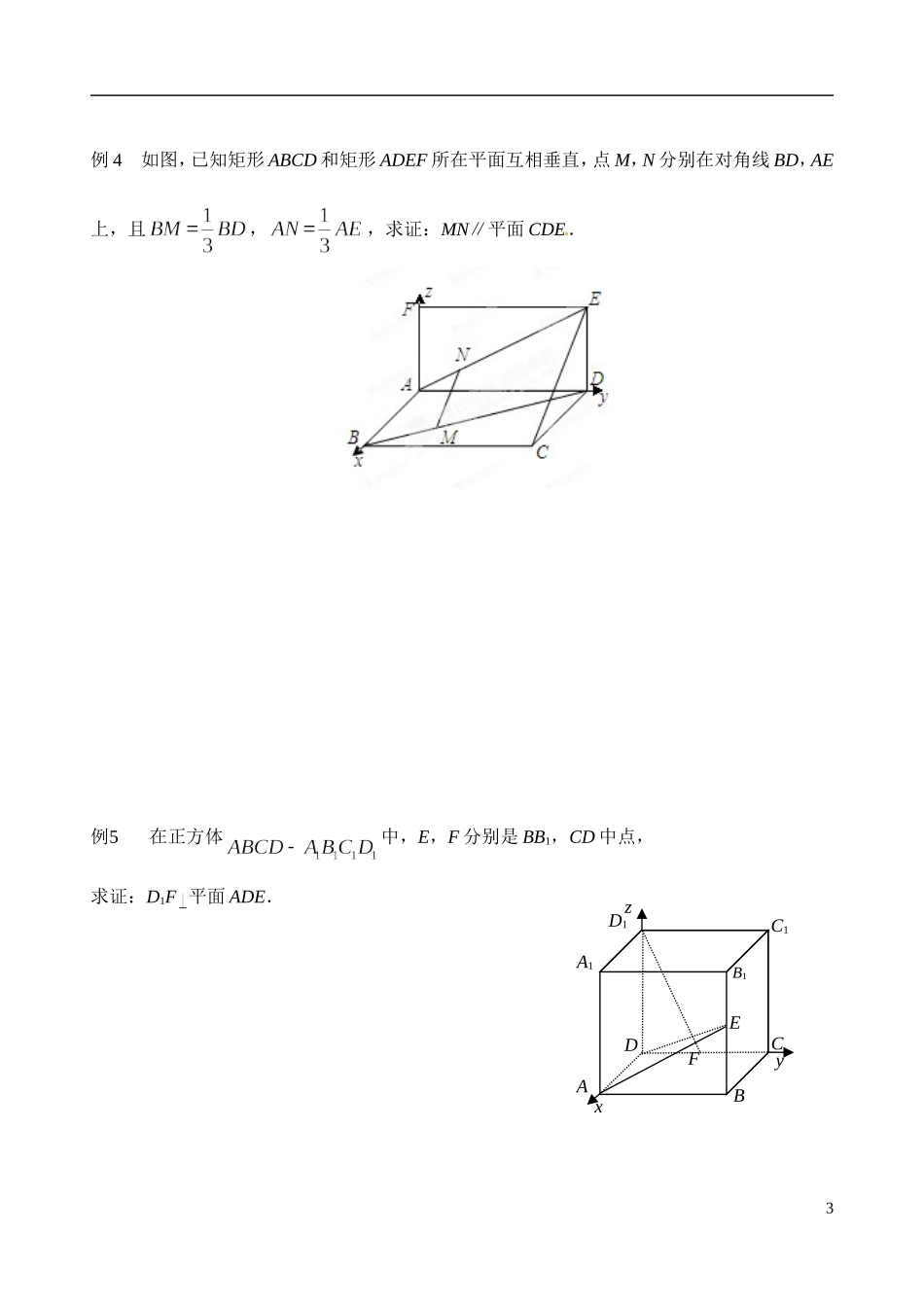
BACDO江苏省灌南高级中学 2014 高二数学 空间线面关系的判定学案问题导学1.在“立体几何初步”一章中,我们研究了空间两条直线、直线与平面、平面现平面的位置关系.相关的判定定理和性质定理是什么?2.上一节,我们定义了空间中直线的方向向量与平面的法向量。那么,我们能不能用直线的方向向量和平面法向量来刻画空间两条直线、直线与平面、平面现平面的关系呢?3.在明确方向向量和法向量含义的基础上,借助图形自己“翻译”完成下表:设空间两条直线 l1,l2的方向向量分别为,,两个平面 α1,α2的法向量分别为,,则有下表:平行垂直l1与 l2l1与 α1α1与 α2典型例题例 1.已知:如图,OB 是平面的斜线,O 为斜足,AB⊥α,A 为垂足,CDα,CD⊥OA.求证:CD⊥OB.1例 3 在直三棱柱中,∠ACD=90°,∠BAC=30°,BC=1,A1A=,M 是 CC1的中点.求证:A1B⊥AM .2zA1xD1B1ADBCC1yEF例 4 如图,已知矩形 ABCD 和矩形 ADEF 所在平面互相垂直,点 M,N 分别在对角线 BD,AE上,且,,求证:MN∥平面 CDE.例5在正方体中,E,F 分别是 BB1,CD 中点,求证:D1F 平面 ADE.3 当堂检测(3)如图,在四棱锥ABCDP 中,底面 ABCD 是正方形,侧棱PD平面 ABCD ,DCPD , E 是 PC 中点,作PBEF 交 PB 于 F .求证:(1)//PA平面 BDE (2)PB平面 DEF4