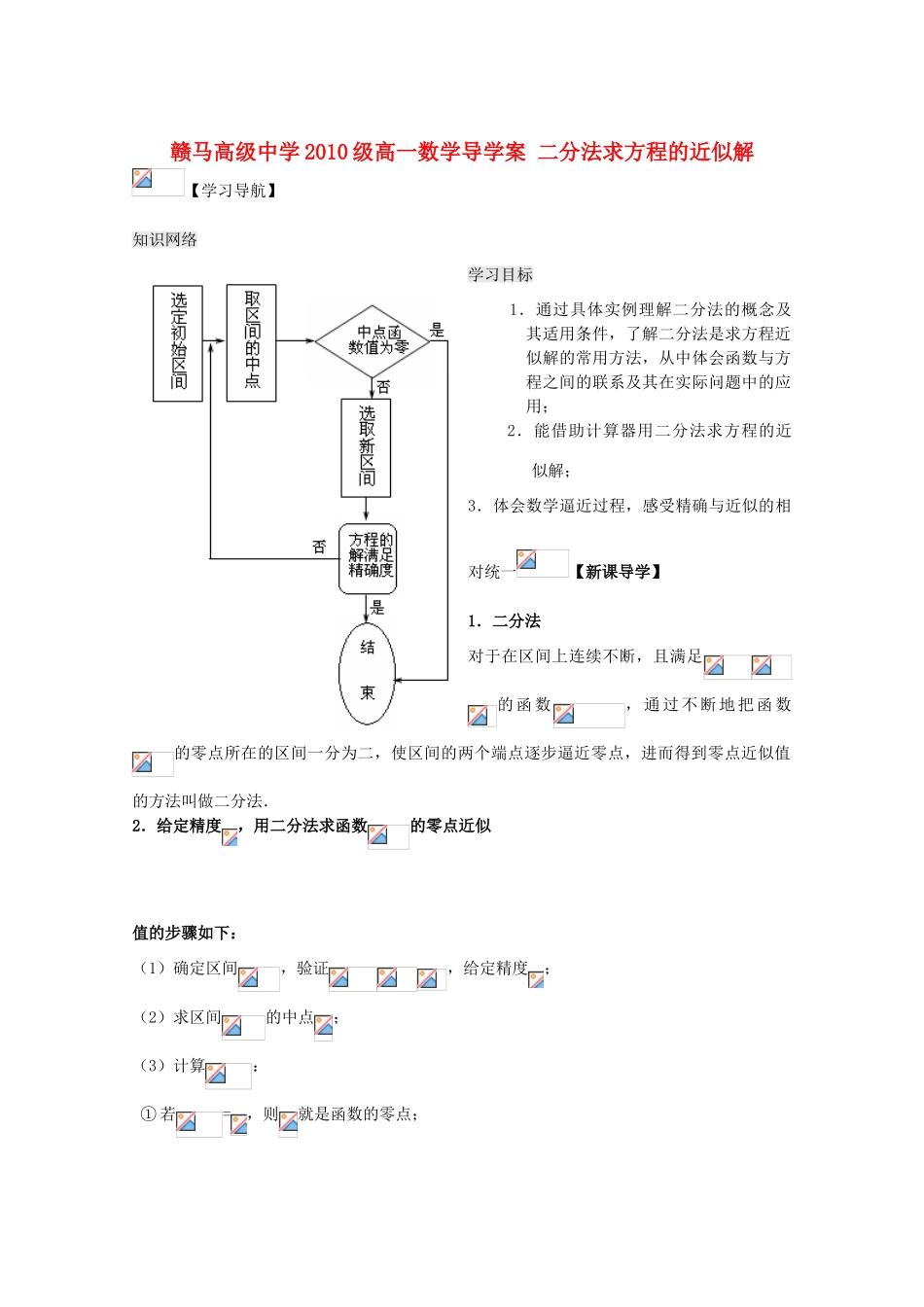
赣马高级中学 2010 级高一数学导学案 二分法求方程的近似解【学习导航】 知识网络 学习目标 1.通过具体实例理解二分法的概念及其适用条件,了解二分法是求方程近似解的常用方法,从中体会函数与方程之间的联系及其在实际问题中的应用;2.能借助计算器用二分法求方程的近似解; 3.体会数学逼近过程,感受精确与近似的相对统一【新课导学】1.二分法对于在区间上连续不断,且满足的 函 数, 通 过 不 断 地 把 函 数的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.2.给定精度,用二分法求函数的零点近似值的步骤如下:(1)确定区间,验证,给定精度;(2)求区间的中点;(3)计算:① 若=,则就是函数的零点;② 若·<,则令=(此时零点);③ 若·<,则令=(此时零点);(4)判断是否达到精度:即若,则得到零点值(或);否则重复步骤2~4.【互动探究】例 1:利用计算器,求方程的一个近似解(精确到 0.1).;例 2:利用计算器,求方程的近似解(精确到 0.1).例 3:利用计算器,求方程的近似解(精确到 0.1).【迁移应用】1. 设是方程的解,则所在的区间为 ( )A. B. C. D.2. 估算方程的正根所在的区间是 ( )A. B. C. D.3.计算器求得方程的负根所在的区间是( )A.(,0) B.C. D.4.利用计算器,求下列方程的近似解(精确到)(1) (2)5. 方 程的 两 个 根 分 别 在 区 间和内 , 则的 取 值 范 围 是 ;6.已知函数,在上存在,使,则实数的取值范围是____ ____________.答案:1.二分法对于在区间上连续不断,且满足的函数,通过不断地把函数的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.2.给定精度,用二分法求函数的零点近似值的步骤如下:(1)确定区间,验证,给定精度;(2)求区间的中点;(3)计算:① 若=,则就是函数的零点;② 若·<,则令=(此时零点);③ 若·<,则令=(此时零点);(4)判断是否达到精度:即若,则得到零点值(或);否则重复步骤2~4.例 1:利用计算器,求方程的一个近似解(精确到 0.1).【解】设,先画出函数图象的简图.(如右图所示)因为,所以在区间内,方程有一解,记为.取与的平均数,因为 ,所以 .再取与的平均数,因为,所以 .如此继续下去,得,因为与精确到的近似值都为,所以此方程的近似解为 ....