江苏省盐城市时杨中学2014届高考数学一轮复习 导数的应用导学案1

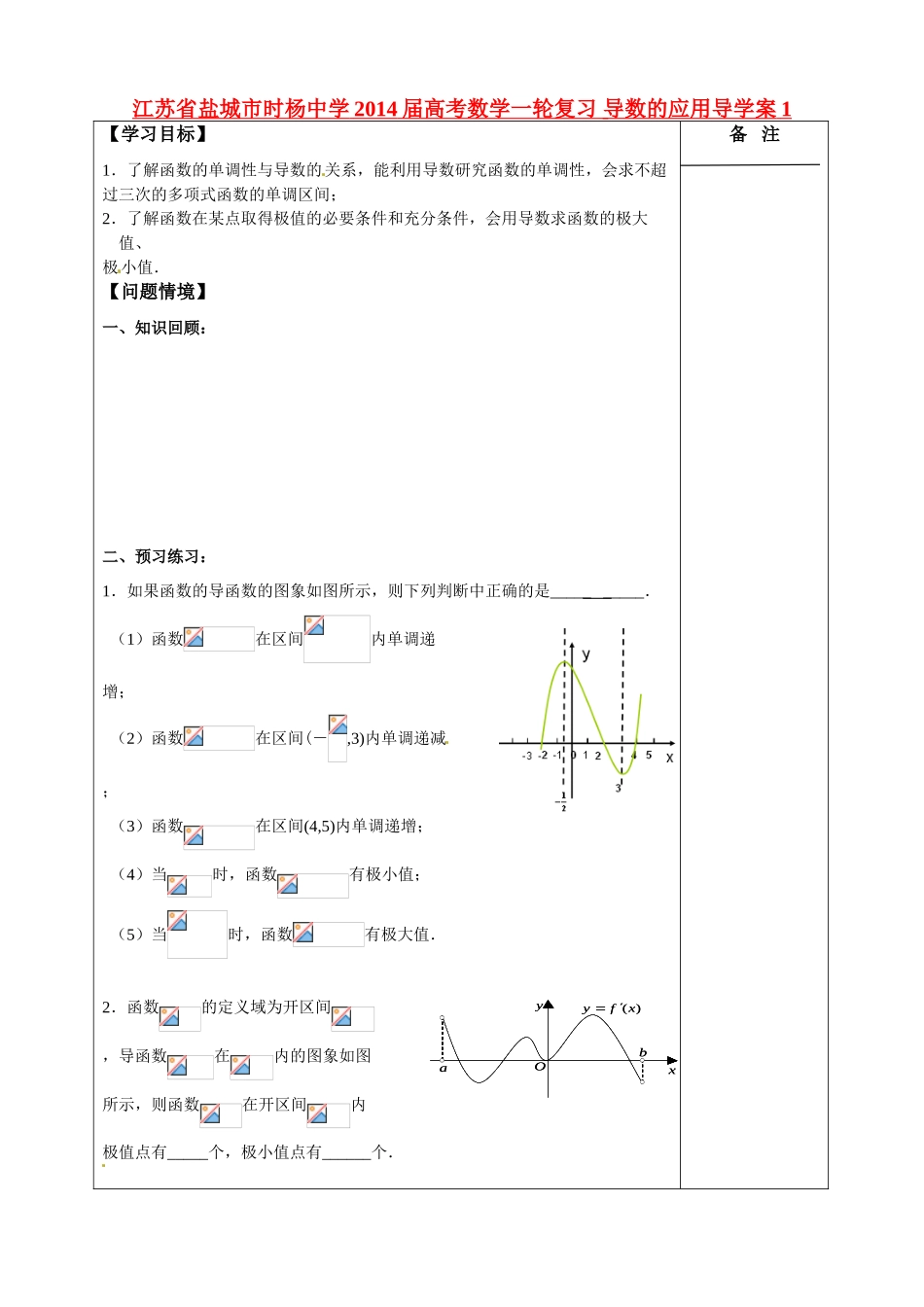
江苏省盐城市时杨中学 2014 届高考数学一轮复习 导数的应用导学案 1 【学习目标】1．了解函数的单调性与导数的关系，能利用导数研究函数的单调性，会求不超过三次的多项式函数的单调区间；2．了解函数在某点取得极值的必要条件和充分条件，会用导数求函数的极大值、极小值．【问题情境】一、知识回顾：二、预习练习：1．如果函数的导函数的图象如图所示，则下列判断中正确的是_____ _____．（1）函数在区间内单调递增；（2）函数在区间(－,3)内单调递减；（3）函数在区间(4,5)内单调递增；（4）当时，函数有极小值；（5）当时，函数有极大值．2．函数的定义域为开区间，导函数在内的图象如图所示，则函数在开区间内极值点有_____个，极小值点有______个．备 注 abxy)(xfyO abxy)(xfyO3．函数在点处有极小值，则=____，=____；的单调增区间是_____________________；单调减区间是_______________． 【我的疑问】 第 1 页共 4 页 【自主探究】1．设，求函数的单调区间．2．设函数，其中。(1)若在处取得极值，求；(2)若在上为增函数，求的范围．备 注【课堂检测】1．已知函数的极大值为 13，则=______．2．若恰有三个单调区间，则的取值范围为____________．3．已知二次函数当时有极值，函数图象过点，且在该点处的切线与垂直，则的单调减区间为 ．4．已知函数在区间内有极值点，则的取值范围为 ．备 注【回标反馈】 第 3 页共 4 页 【巩固练习】1.函数的极大值为________，极小值为_________．2．函数在区间上是减函数，则的取值范围为___________．3．函数的图像在点处的切线方程为．（1）求函数的解析式；（2）求函数的单调区间．4．函数在处有极值，极大值为 4，极小值为 0，求的值．备 注第 4 页共 4 页