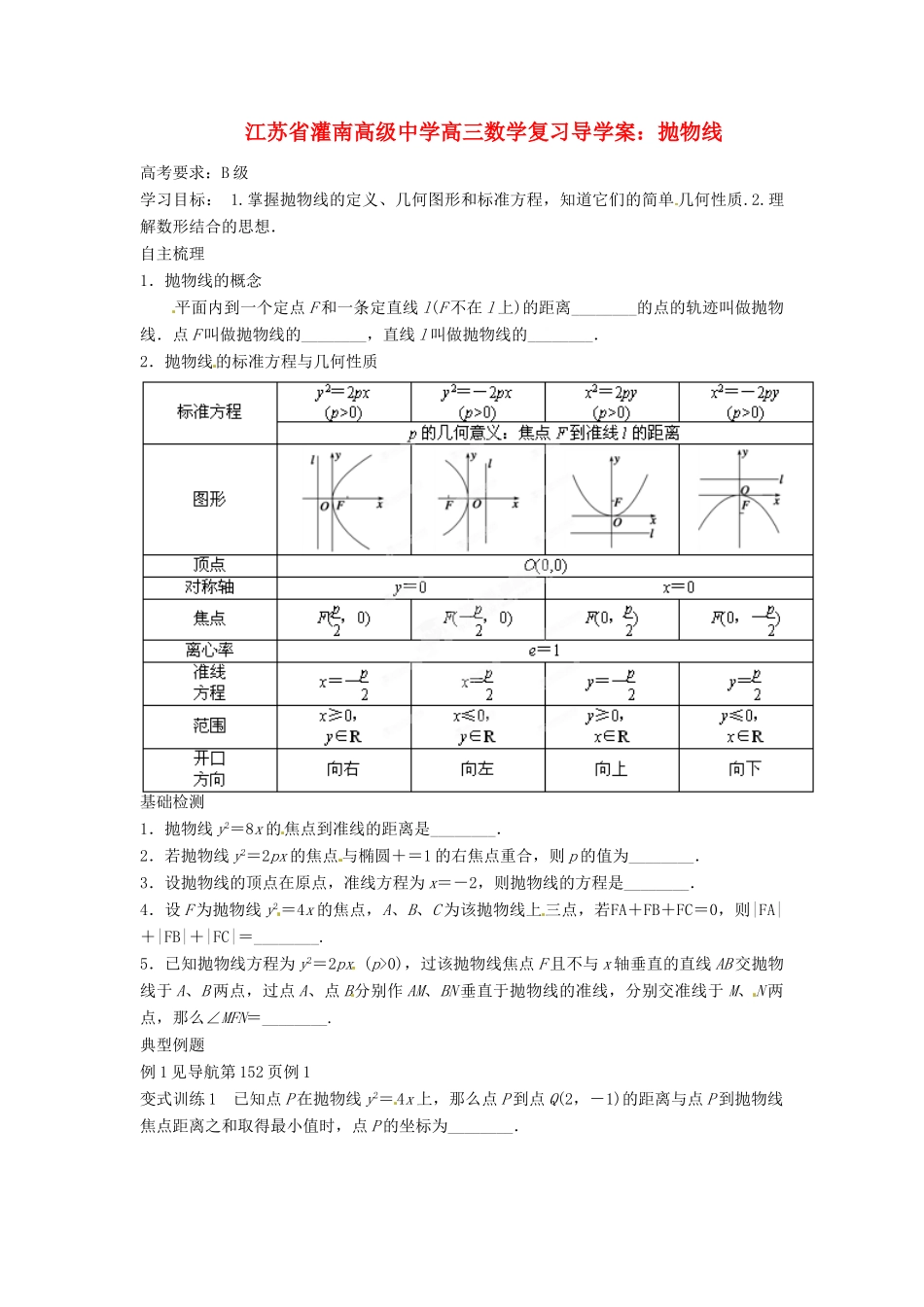
江苏省灌南高级中学高三数学复习导学案:抛物线高考要求:B 级学习目标: 1.掌握抛物线的定义、几何图形和标准方程,知道它们的简单 几何性质.2.理解数形结合的思想. 自主梳理1.抛物线的概念平面内到一个定点 F 和一条定直线 l(F 不在 l 上)的距离________的点的轨迹叫做抛物线.点 F 叫做抛物线的________,直线 l 叫做抛物线的________.2.抛物线的标准方程与几何性质基础检测1.抛物线 y2=8x 的焦点到准线的距离是________.2.若抛物线 y2=2px 的焦点 与椭圆+=1 的右焦点重合,则 p 的值为________.3.设抛物线的顶点在原点,准线方程为 x=-2,则抛物线的方程是________.4.设 F 为抛物线 y2=4x 的焦点,A、B、C 为该抛物线上 三点,若FA+FB+FC=0,则|FA|+|FB|+|FC|=________.5.已知抛物线方程为 y2=2px (p>0),过该抛物线焦点 F 且不与 x 轴垂直的直线 AB 交抛物线于 A、B 两点,过点 A、点 B分别作 AM、BN 垂直于抛物线的准线,分别交准线于 M、 N 两点,那么∠MFN=________.典型例题例 1 见导航第 152 页例 1变式训练 1 已知点 P 在抛物线 y2=4x 上,那么点 P 到点 Q(2,-1)的距离与点 P 到抛物线焦点距离之和取得最小值时,点 P 的坐标为________.例 2 已知抛物线的顶点在原点,焦点在 y 轴上,抛物线上一点 M(m,-3)到焦点的距离为5,求 m 的值、抛物线方程和准线方程.变式训练 2 根据下列条件求抛物线的标准方程:(1)抛物线的焦点 F 是双曲线 16x2-9y2=144 的左顶点;(2)过点 P(2,-4).变 式 训 练 3 已 知 AB 是 抛 物 线 y2 = 2px (p>0) 的 焦 点 弦 , F 为 抛 物 线 的 焦 点 ,A(x1,y1),B(x2,y2).求证:(1)x1x2=;(2)+为定值.