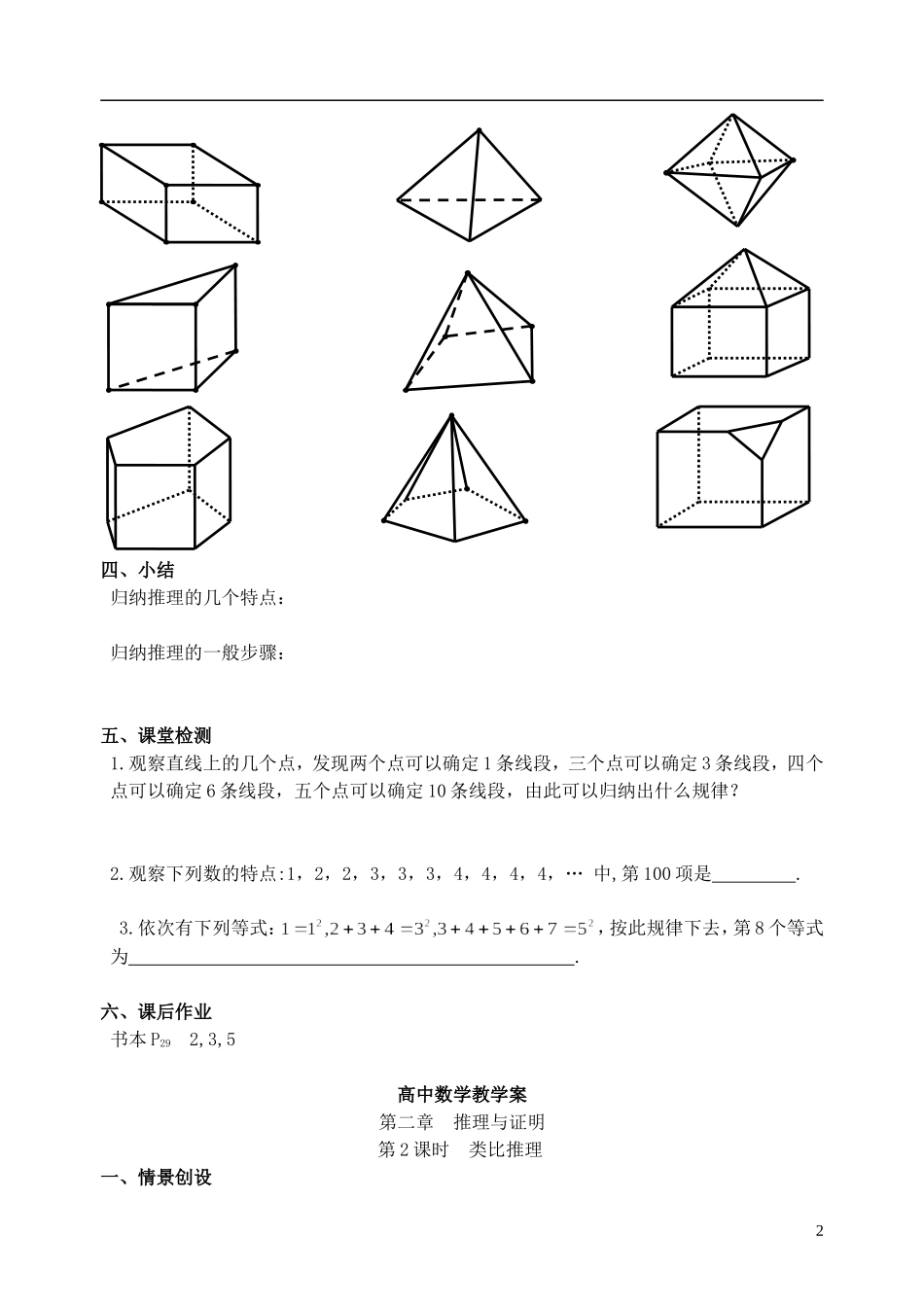
高中数学教学案第二章 推理与证明第 1 课时 归纳推理一、情景创设1.西汉时期的马王堆女尸,距今已将近 2200 年,是根据同位素的半衰期的推测的。2.哥德巴赫,德国数学家。1742 年 6 月 7 日,他在写给著名数学家欧拉的一封信中,提出了两个大胆的猜想:(1)任何不小于 6 的偶数,都是两个奇质数之和:(2)任何不小于 9 的奇数,都是 3 个奇质数之和.这就是数学史上著名的“哥德巴赫猜想”. (3)蛇是用肺呼吸的,鳄鱼是用肺呼吸的,海归是用肺呼吸的,蜥蜴是用肺呼吸的,蛇、鳄鱼、海归、蜥蜴都是爬行动物,所以,所有的爬行动物都是用肺呼吸的.(4)教师从口袋里第一次拿出一块糖,第二次又拿出一块糖,第三次又拿出一块糖,第四次…….二、建构数学归纳推理:归纳推理的一般模式:三、数学应用例 1.三角形的内角和是 1800,凸四边形的内角和是 3600,凸五边形的内角和是 5400,请猜想:凸 n 边形的内角和是 练习.由此我们猜想: 并证明你的结论.练习.数一数图中的凸多面体的面数 F、顶点数 V 和棱数 E,然后用归纳法推理得出它们之间的关系为 .1四、小结归纳推理的几个特点:归纳推理的一般步骤:五、课堂检测1.观察直线上的几个点,发现两个点可以确定 1 条线段,三个点可以确定 3 条线段,四个点可以确定 6 条线段,五个点可以确定 10 条线段,由此可以归纳出什么规律?2.观察下列数的特点:1,2,2,3,3,3,4,4,4,4,… 中,第 100 项是 .3.依次有下列等式:,按此规律下去,第 8 个等式为 .六、课后作业书本 P29 2,3,5高中数学教学案第二章 推理与证明第 2 课时 类比推理一、情景创设21.据传,春秋时代鲁国的公输班受到路边的齿形草能割破行人的腿的启发,发明了锯子.他的思维过程为:齿形草能割破行人的腿,“锯子”能“锯”开木材,它们功能上是类似的.因此,它们形状上也应该类似,“锯子”应该是齿形的.2.仿照鱼类的外型和它们在水中沉浮的原理,发明了潜水艇.3.利用平面几何的本定理类比得到立体几何中的基本定理.二、建构数学类比推理:类比推理的一般模式:三.应用数学例 1.(1)试根据等式的性质猜想不等式的性质.(2)类比实数中的加法与乘法,他们有哪些类似的性质?练习.试将平面上的圆与空间中的球进行类比。例 2.类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想.3练习:(2001 年上海)已知两个圆① x2+y2=1:与② x2+(y-3)2=1,则由①式减去②式可得上...