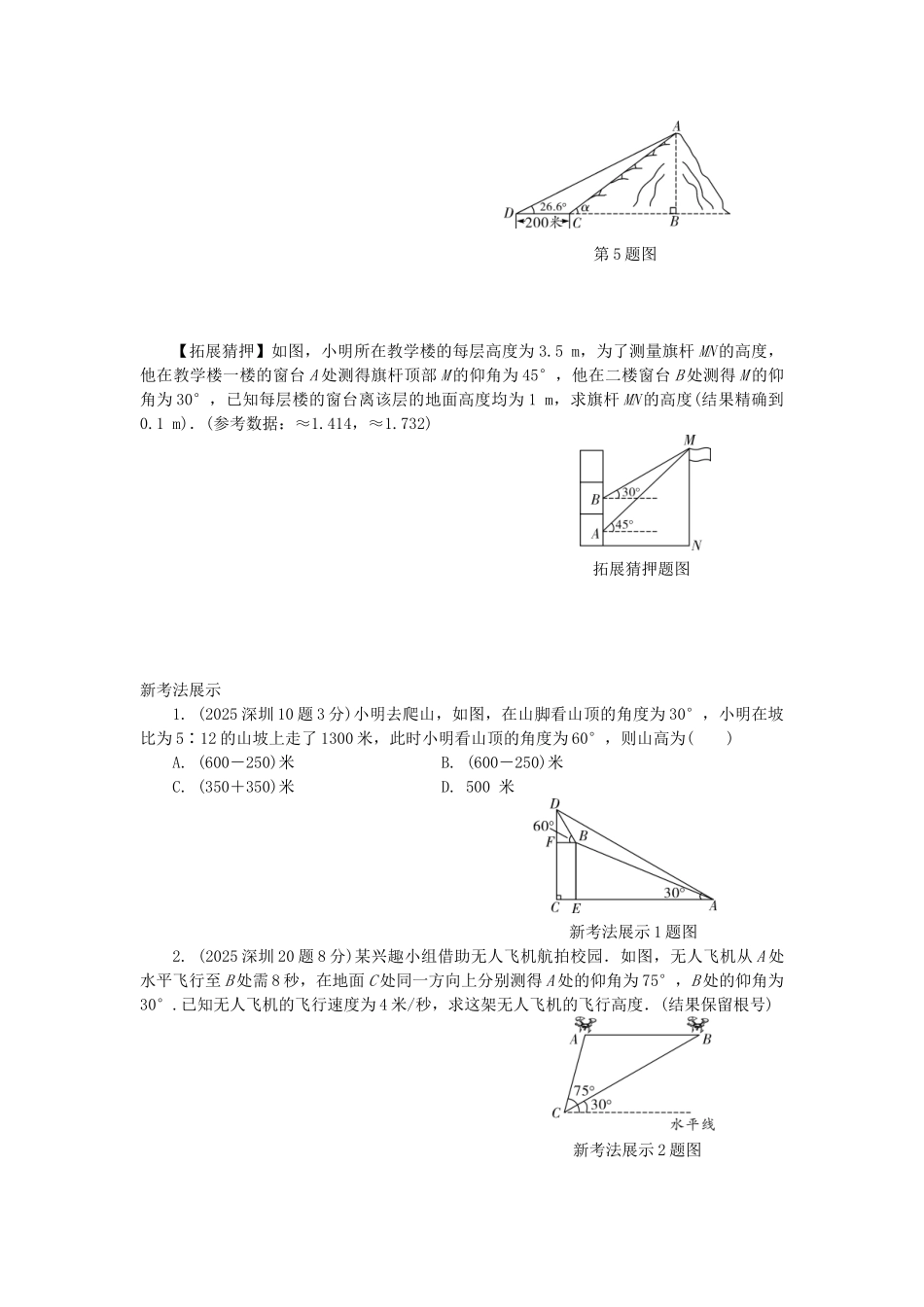
第四章 三角形第六节 解直角三角形及其应用玩转广东省卷 6 年中考真题(2025~2025)命题点 1 锐角三角函数(省卷 6 年 2 考)1. (2025 省卷 8,3 分)如图,在平面直角坐标系中,点 A 的坐标为(4,3),那么cosα 的值是( )A. B. C. D. 2. (2025 省卷 14,4 分)在 Rt△ABC 中,∠ABC=90°,AB=3,BC=4,则 sinA=________.命题点 2 解直角三角形(省卷 6 年 2 考)3. (2025 省 卷 21 , 7 分 ) 如 图 , Rt△ACB 中 , ∠ B =30°,∠ACB=90°,CD⊥AB 交 AB 于 D.以 CD 为较短的直角边向△CDB 的同侧作 Rt△DEC,满足∠E=30°,∠DCE=90°,再用同样的方法作 Rt△FGC,∠FCG=90°,继续用同样的方法作 Rt△HIC,∠HCI=90°.若 AC=a,求 CI 的长. 第 3 题图命题点 3 (省卷 6 年 3 考)4. (2025 省卷 20,7 分)如图,某数学兴趣小组想测量一棵树 CD 的高度,他们先在点A 处测得树顶 C 的仰角为 30°,然后沿 AD 方向前行 10 m,到达 B 点,点 B 处测得树顶 C 的仰角为 60°(A、B、D 三点在同一直线上).请你根据他们的测量数据计算这棵树 CD 的高度(结果精确到 0.1 m).(参考数据:≈1.414,≈1.732) 第 4 题图5. (2025 省卷 18,7 分)如图,小山岗的斜坡 AC 的坡度是 tanα=,在与山脚 C 距离200 米的 D 处,测得山顶 A 的仰角为 26.6°,求小山岗的高 AB(结果取整数;参考数据:sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50). 第 5 题图【拓展猜押】如图,小明所在教学楼的每层高度为 3.5 m,为了测量旗杆 MN 的高度,他在教学楼一楼的窗台 A 处测得旗杆顶部 M 的仰角为 45°,他在二楼窗台 B 处测得 M 的仰角为 30°,已知每层楼的窗台离该层的地面高度均为 1 m,求旗杆 MN 的高度(结果精确到0.1 m).(参考数据:≈1.414,≈1.732) 拓展猜押题图新考法展示1. (2025 深圳 10 题 3 分)小明去爬山,如图,在山脚看山顶的角度为 30°,小明在坡比为 5∶12 的山坡上走了 1300 米,此时小明看山顶的角度为 60°,则山高为( )A. (600-250)米 B. (600-250)米C. (350+350)米 D. 500 米 新考法展示 1 题图2. (2025 深圳 20 题 8 分)某兴趣小组借助无人飞机航拍校园.如图,无人飞机从 A 处水平飞行至 B 处需 8 秒,在地面 C 处同一方向上分别测得...