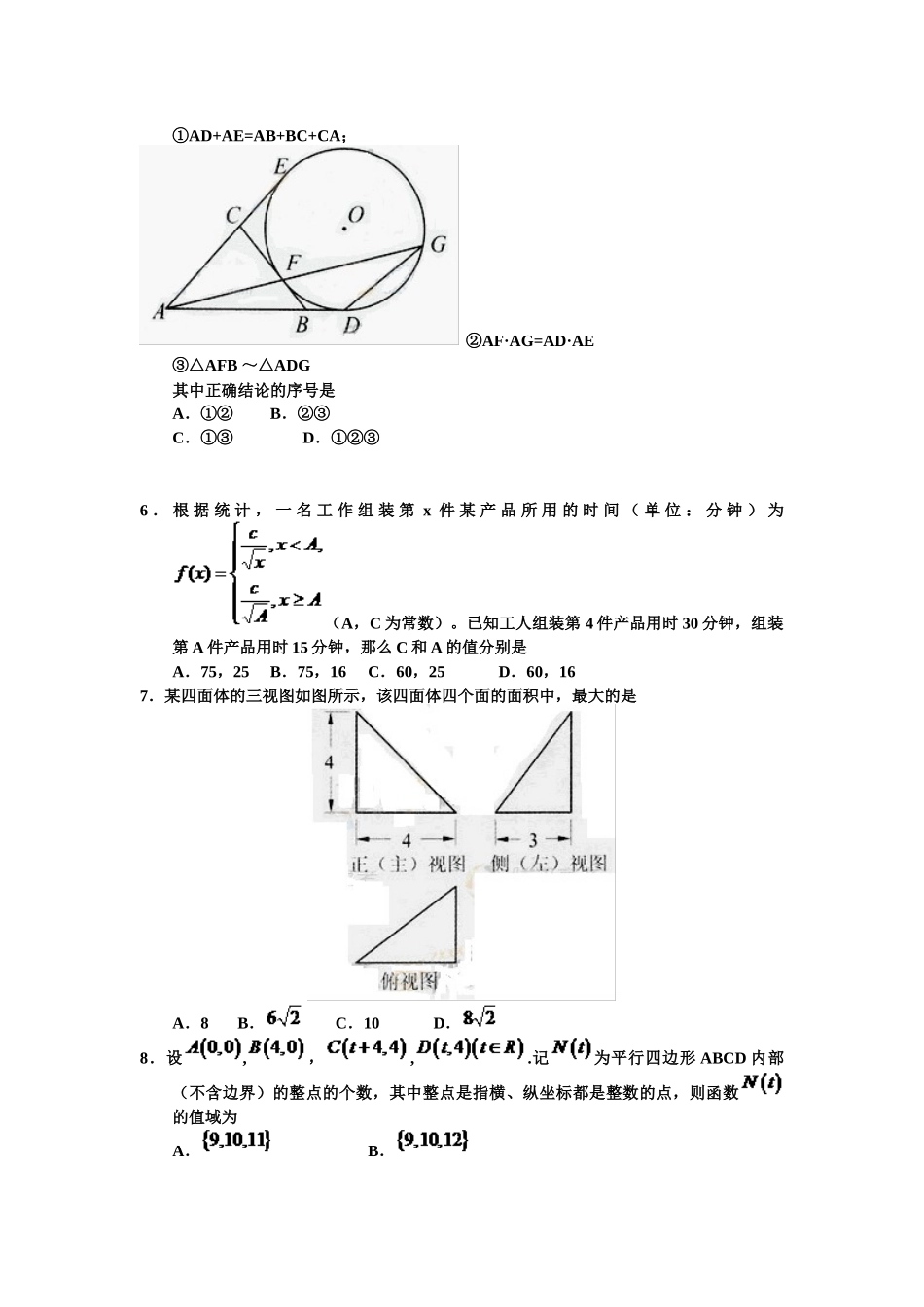
2025 年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共 5 页,150 分。考试时间长 120 分钟。考生务必将答案答在答题卡上,在试卷上作答无效。考试结束后,将本试卷和答题卡一并交回。第一部分(选择题 共 40 分)一、选择题共 8 小题,每小题 5 分,共 40 分。在每小题列出的四个选项中,选出符合题目要求的一项。1.已知集合 P={x︱x2≤1},M={a}.若 P∪M=P,则 a 的取值范围是A.(-∞, -1] B.[1, +∞) C.[-1,1] D.(-∞,-1] ∪[1,+∞)2.复数A.i B.-i C. D.3.在极坐标系中,圆 ρ=-2sinθ 的圆心的极坐标系是A. B. C. (1,0) D.(1,)4.执行如图所示的程序框图,输出的 s 值为A.-3B.-C.D.25.如图,AD,AE,BC 分别与圆 O 切于点 D,E,F,延长 AF 与圆 O 交于另一点 G。给出下列三个结论:①AD+AE=AB+BC+CA;②AF·AG=AD·AE③△AFB ~△ADG其中正确结论的序号是A.①② B.②③C.①③ D.①②③6 . 根 据 统 计 , 一 名 工 作 组 装 第 x 件 某 产 品 所 用 的 时 间 ( 单 位 : 分 钟 ) 为 (A,C 为常数)。已知工人组装第 4 件产品用时 30 分钟,组装第 A 件产品用时 15 分钟,那么 C 和 A 的值分别是A.75,25 B.75,16 C.60,25 D.60,167.某四面体的三视图如图所示,该四面体四个面的面积中,最大的是A.8 B. C.10 D.8.设,,,.记为平行四边形 ABCD 内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数的值域为A. B.C. D.第二部分 (非选择题 共 110 分)二、填空题共 6 小题,每小题 5 分,共 30 分。9 . 在中 。 若b=5 ,, tanA=2 , 则sinA=____________ ;a=_______________。10.已知向量 a=(,1),b=(0,-1),c=(k,)。若 a-2b 与 c 共线,则k=___________________。11.在等比数列{an}中,a1=,a4=-4,则公比 q=______________;____________。12.用数字 2,3 组成四位数,且数字 2,3 至少都出现一次,这样的四位数共有__________个。(用数字作答)13.已知函数若关于 x 的方程 f(x)=k 有两个不同的实根,则数 k 的取值范围是_______14.曲线 C 是平面内与两个定点 F1(-1,0)和 F¬2(1,0)的距离的积等于常数的点的轨迹.给出下列三个结论:① 曲线 C 过坐标原点;② 曲线 C 关...