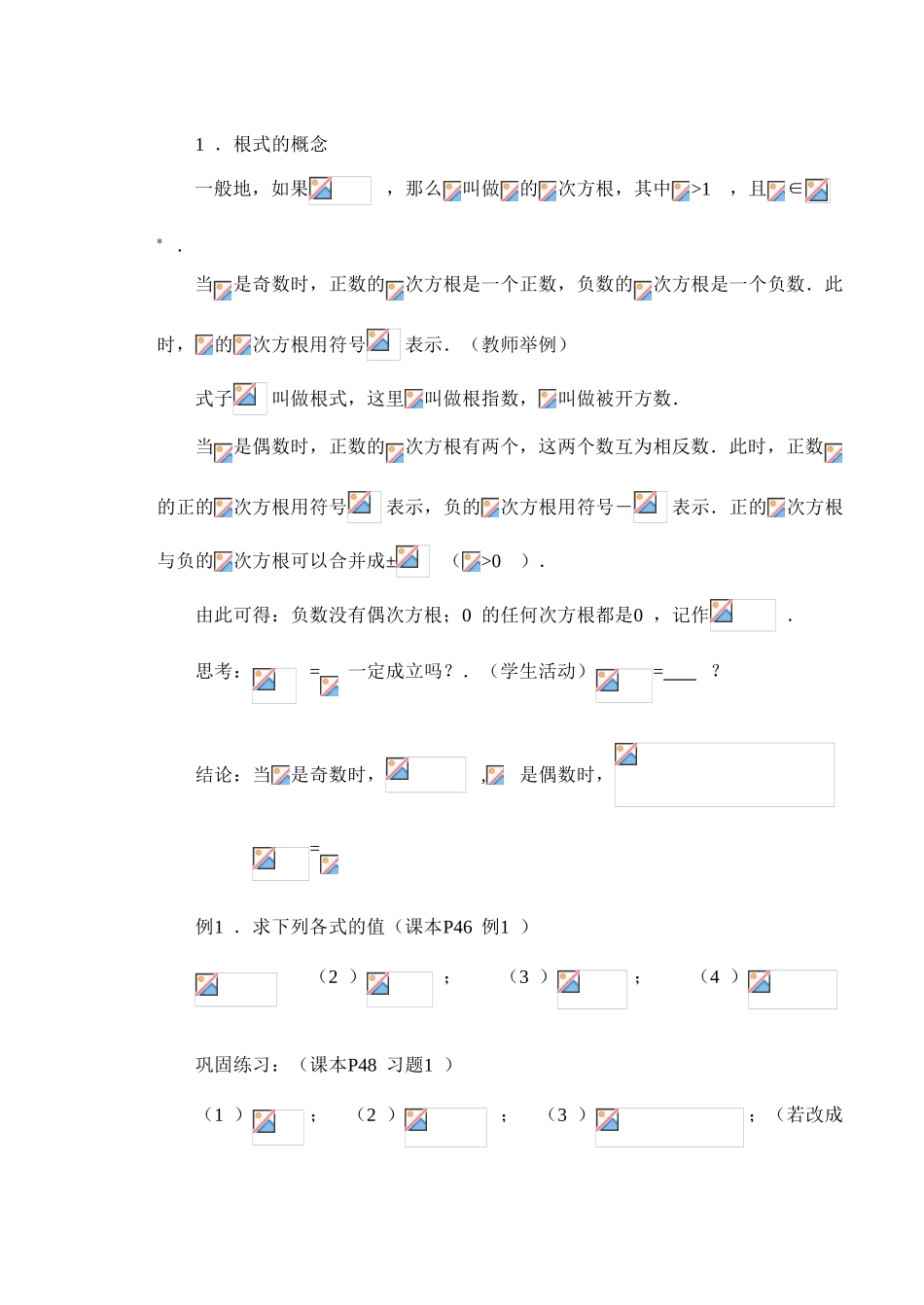
课 题 : §2.2.1 分 数 指 数 幂主 备 人 丁 文 玲教 学 目 的 :(1 )掌握根式的概念;(2 )规定分数指数幂的意义;(3 )学会根式与分数指数幂之间的相互转化;(4 )理解有理指数幂的含义及其运算性质;(5 )了解无理数指数幂的意义教 学 重 点 :分数指数幂的意义,根式与分数指数幂之间的相互转化,有理指数幂的运算性质教 学 难 点 :根式的概念,根式与分数指数幂之间的相互转化,了解无理数指数幂. 教学过程:一 、引 入 课 题1 .由实例引入,了解指数概念提出的背景,体会引入指数的必要性;2 .复习初中整数指数幂的运算性质;3 .初中根式的概念;如果一个数的平方等于a ,那么这个数叫做a 的平方根,如果一个数的立方等于a ,那么这个数叫做a 的立方根;二 、新 课 教 学(一)指数与指数幂的运算1 .根式的概念一般地,如果,那么叫做的次方根,其中>1,且∈* .当是奇数时,正数的次方根是一个正数,负数的次方根是一个负数.此时,的次方根用符号表示.(教师举例)式子叫做根式,这里叫做根指数,叫做被开方数.当是偶数时,正数的次方根有两个,这两个数互为相反数.此时,正数的正的次方根用符号表示,负的次方根用符号-表示.正的次方根与负的次方根可以合并成±(>0).由此可得:负数没有偶次方根;0 的任何次方根都是0 ,记作.思考:=一定成立吗?.(学生活动)= ?结论:当是奇数时,,是偶数时,=例1 .求下列各式的值(课本P46 例1 ) (2 ); (3 ); (4 )巩固练习:(课本P48 习题1 )(1 ); (2 ); (3 );(若改成< 呢?)(4 )2 .分数指数幂正数的分数指数幂的意义规定:0 的正分数指数幂等于0 ,0 的负分数指数幂没有意义指出:规定了分数指数幂的意义后,指数的概念就从整数指数推广到了有理数指数,那么整数指数幂的运算性质也同样可以推广到有理数指数幂.3 .有理指数幂的运算性质(1 )·;(2 );(3 ).引导学生解决本课开头实例问题例2 .(课本P47、例2 、3 )1 .求下列各式的值(1 ); (2 ); (3 );(4 )2 .用分数指数幂表示下列各式()(1 ); (2 )说明:让学生熟练掌握根式与分数指数幂的互化和有理指数幂的运算性质运用.巩固练习:(课本P47 练习1—3学生直接做在书上)4 .无理指数幂结合教材P47利用逼近的思想理解无理指数幂的意义.指出:一般地,无理数指数幂...