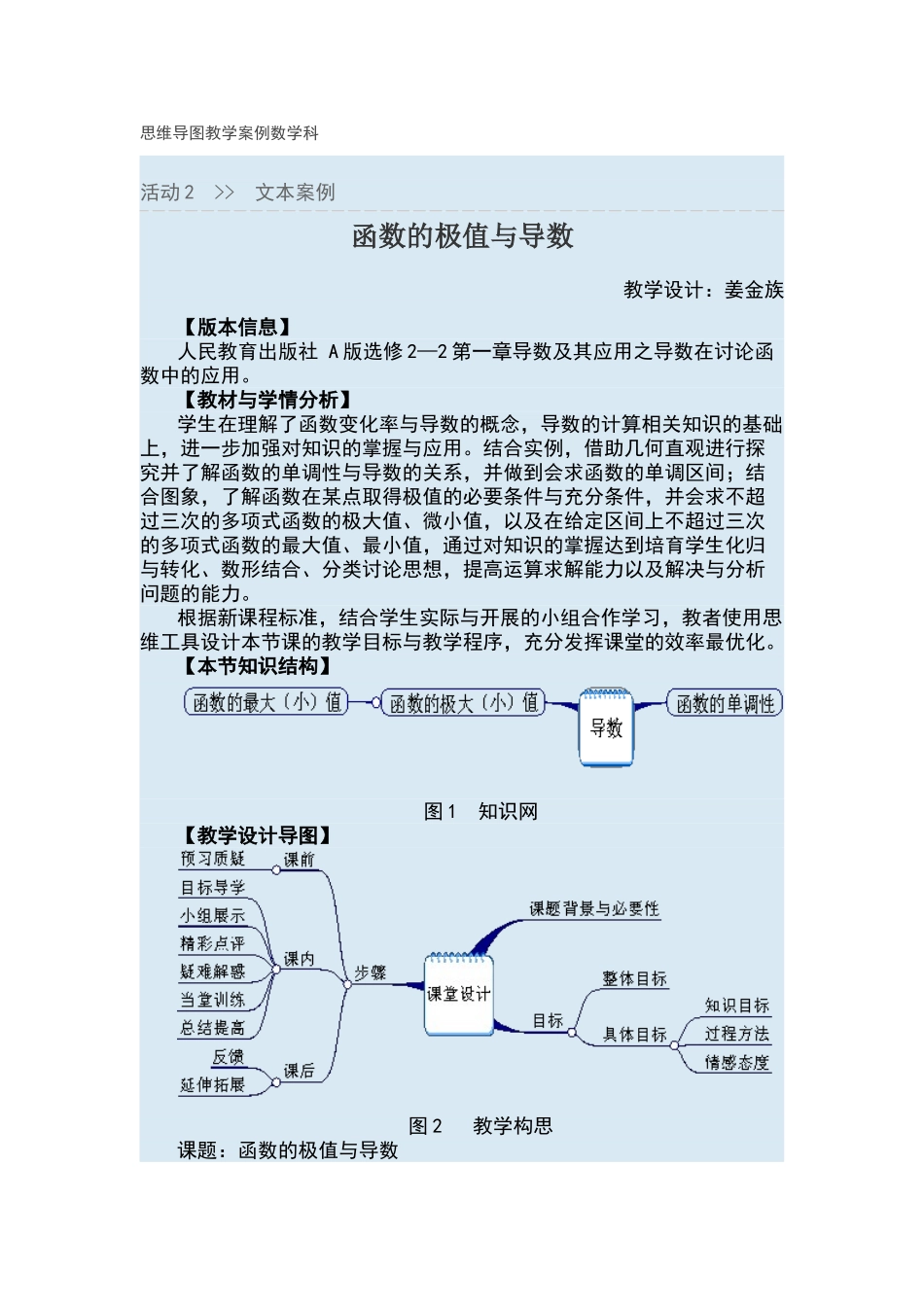
思维导图教学案例数学科活动 2 >> 文本案例函数的极值与导数教学设计:姜金族【版本信息】人民教育出版社 A 版选修 2—2 第一章导数及其应用之导数在讨论函数中的应用。【教材与学情分析】学生在理解了函数变化率与导数的概念,导数的计算相关知识的基础上,进一步加强对知识的掌握与应用。结合实例,借助几何直观进行探究并了解函数的单调性与导数的关系,并做到会求函数的单调区间;结合图象,了解函数在某点取得极值的必要条件与充分条件,并会求不超过三次的多项式函数的极大值、微小值,以及在给定区间上不超过三次的多项式函数的最大值、最小值,通过对知识的掌握达到培育学生化归与转化、数形结合、分类讨论思想,提高运算求解能力以及解决与分析问题的能力。根据新课程标准,结合学生实际与开展的小组合作学习,教者使用思维工具设计本节课的教学目标与教学程序,充分发挥课堂的效率最优化。【本节知识结构】图 1 知识网【教学设计导图】图 2 教学构思课题:函数的极值与导数一、教学目标教学目标确立思路(思维工具:目标分析法、可能性分析法、优先分析法):首先,确立整体目标。根据教材特点,教者计划把本节课设计成探究课,突出观察、分析、类比、归纳、综合等思维能力训练。其次,围绕三维目标(知识与技能、过程与方法、情感态度与价值观)要求,在充分考虑多种目标可能性的基础上,优先确立以下三个教学目标:1、了解函数极值的概念,以及在闭区间上函数最值的概念。2、结合图象,了解函数在某点取得极值的必要和充分条件,会求函数的极大值与微小值,会求函数在闭区间上的最值(多项式函数不超过三次)3、培育数形结合的思想方法,体会数学图形结构美,提高学习热情.重点:利用导数求函数的极值难点:函数在某点取得极值的必要条件与充分条件.教学步骤二、课前预习,发现问题:(因素分析法)阅读课本 P26-29 止,思考回答下列问题:(使用三维分析法)1.观察课本P27 图与图当 t=a 时,函数 h(t)的导数的值为多少此点附近的图像有什么特点导数的符号有什么变化规律2.观察 27 页中间两个图像,回答下列问题:(1)在 a,b,c,d,f,g,h 等点的函数值与这些点附近的函数值有什么关系(2)函数在这些点的导数值为多少这些点附近,导数的符号有什么规律3、你如何定义一个函数的微小值点,微小值以及极大值点,极大值定义:_________________________________________________三、预习自测:(其他人的观点换位分析法)1....