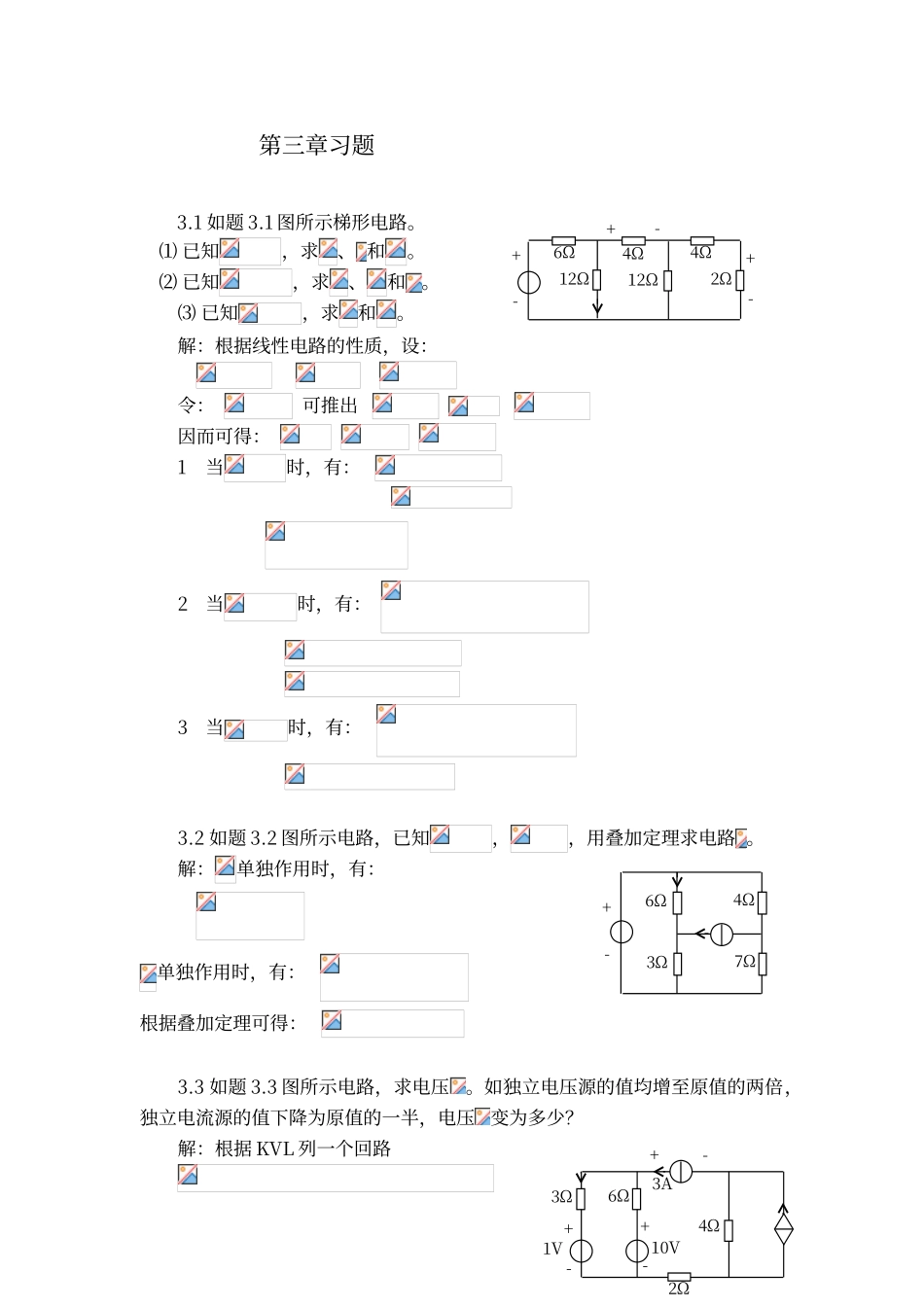
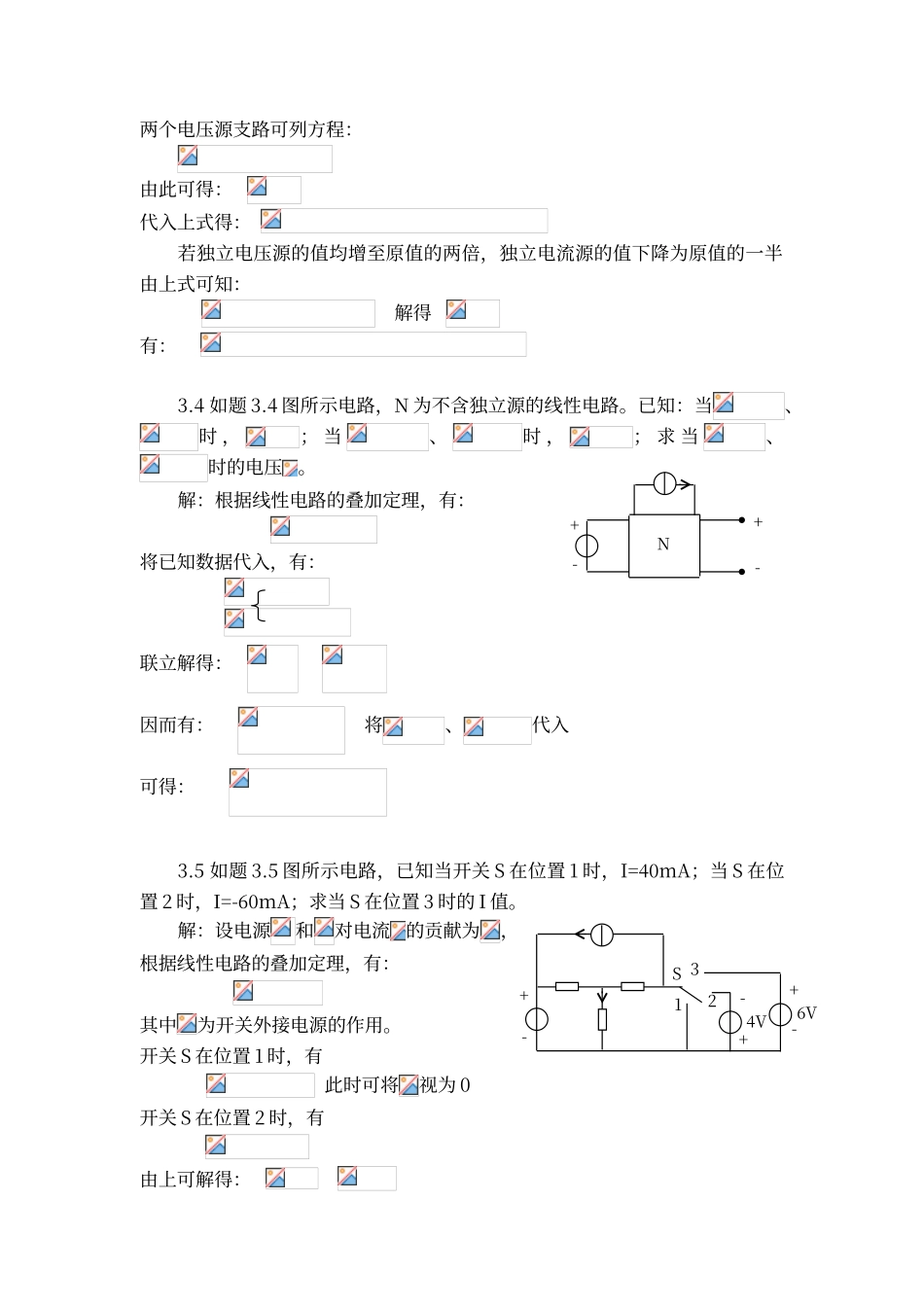
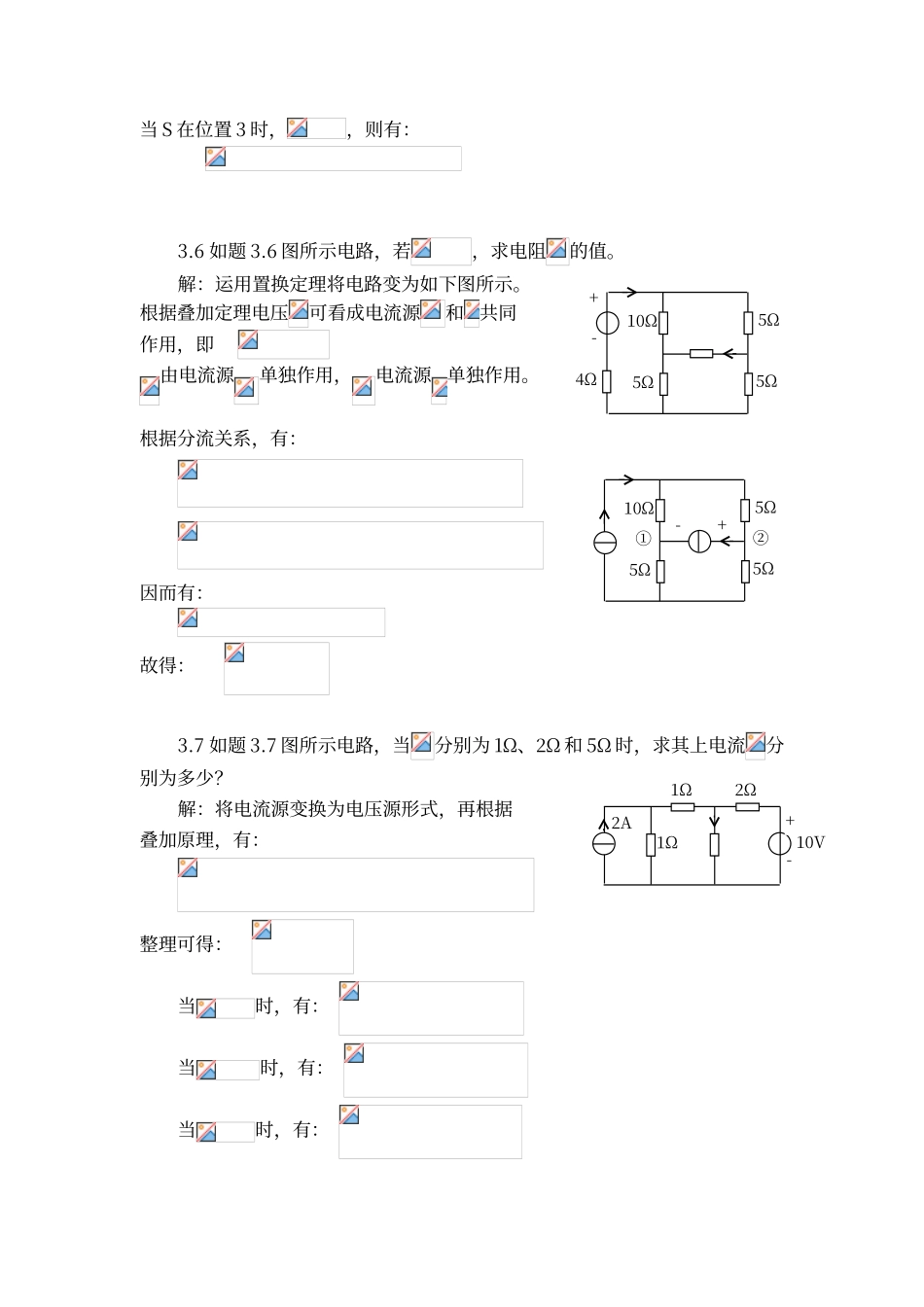
第三章习题3.1 如题 3.1 图所示梯形电路。 ⑴ 已知,求、 和。 ⑵ 已知,求、和。⑶ 已知,求和。解:根据线性电路的性质,设: 令: 可推出 因而可得: 1当时,有: 2当时,有: 3当时,有: 3.2 如题 3.2 图所示电路,已知,,用叠加定理求电路 。解:单独作用时,有: 单独作用时,有: 根据叠加定理可得: 3.3 如题 3.3 图所示电路,求电压。如独立电压源的值均增至原值的两倍,独立电流源的值下降为原值的一半,电压变为多少?解:根据 KVL 列一个回路+-6Ω12Ω+-4Ω12Ω4Ω2Ω-+6Ω3Ω-+7Ω4Ω+-3Ω2Ω-+1V6Ω-+10V3A4Ω两个电压源支路可列方程:由此可得: 代入上式得: 若独立电压源的值均增至原值的两倍,独立电流源的值下降为原值的一半由上式可知: 解得 有: 3.4 如题 3.4 图所示电路,N 为不含独立源的线性电路。已知:当、时 ,; 当、时 ,; 求 当、时的电压。解:根据线性电路的叠加定理,有:将已知数据代入,有: 联立解得: 因而有: 将、代入可得: 3.5 如题 3.5 图所示电路,已知当开关 S 在位置 1 时,I=40mA;当 S 在位置 2 时,I=-60mA;求当 S 在位置 3 时的 I 值。解:设电源和对电流的贡献为,根据线性电路的叠加定理,有: 其中为开关外接电源的作用。开关 S 在位置 1 时,有 此时可将视为 0开关 S 在位置 2 时,有 由上可解得: -+-+N-+S132-+4V-+6V当 S 在位置 3 时,,则有: 3.6 如题 3.6 图所示电路,若,求电阻的值。解:运用置换定理将电路变为如下图所示。根据叠加定理电压可看成电流源和共同作用,即 由电流源单独作用,电流源单独作用。根据分流关系,有:因而有:故得: 3.7 如题 3.7 图所示电路,当分别为 1Ω、2Ω 和 5Ω 时,求其上电流分别为多少?解:将电流源变换为电压源形式,再根据叠加原理,有:整理可得: 当时,有: 当时,有: 当时,有: 4Ω-10Ω5Ω+5Ω5Ω2A1Ω1Ω2Ω-10V+②①-+10Ω5Ω5Ω5Ω3.8 如题 3.8 图所示电路,N 为不含独立源的线性电路,已知输出电压;若在输出端接上 5Ω 电阻,则。问在输出端接 3Ω 电阻时,输出电压与输入电压的关系如何?解:从输出端进行戴文宁等效,有当时,,可得 当时,,代入上式可求得: 因此,当时,有 3.9 如题 3.9 图所示电路,当 R=12Ω 时其上电流为 I。若要求 I 增至原来值的 3 倍,而电路中除 R 外的其他部分均不...