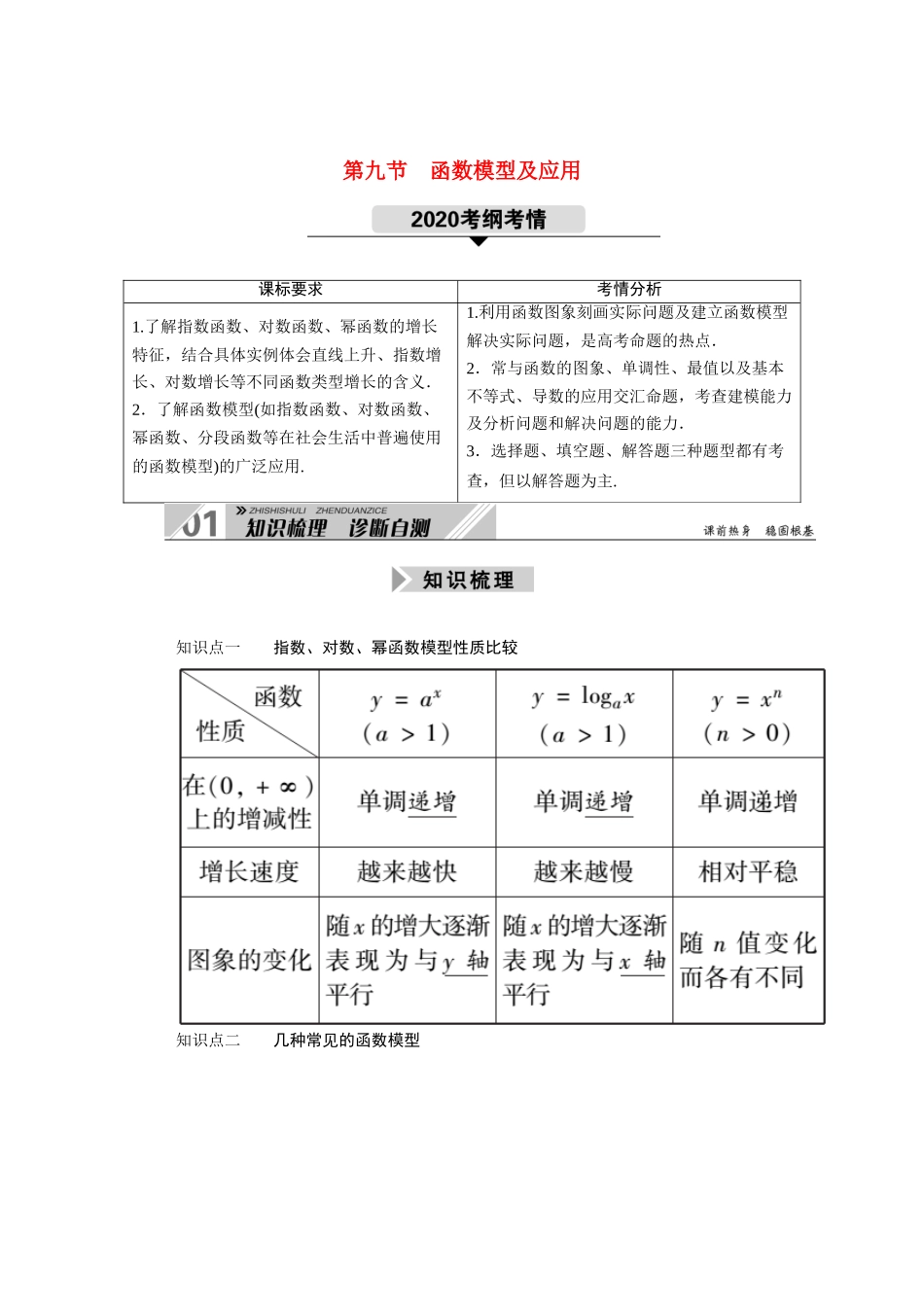
第九节 函数模型及应用课标要求考情分析1.了解指数函数、对数函数、幂函数的增长特征,结合具体实例体会直线上升、指数增长、对数增长等不同函数类型增长的含义.2.了解函数模型(如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型)的广泛应用.1.利用函数图象刻画实际问题及建立函数模型解决实际问题,是高考命题的热点.2.常与函数的图象、单调性、最值以及基本不等式、导数的应用交汇命题,考查建模能力及分析问题和解决问题的能力.3.选择题、填空题、解答题三种题型都有考查,但以解答题为主.知识点一 指数、对数、幂函数模型性质比较知识点二 几种常见的函数模型(1)“直线上升”是匀速增长,其增长量固定不变;“指数增长”先慢后快,其增长量成倍增加,常用“指数爆炸”来形容;“对数增长”先快后慢,其增长速度缓慢.(2)充分理解题意,并熟练掌握几种常见函数的图象和性质是解题的关键.(3)易忽视实际问题中自变量的取值范围,需合理确定函数的定义域,必须验证数学结果对实际问题的合理性.1.思考辨析判断下列结论正误(在括号内打“√”或“×”)(1)某种商品进价为每件 100 元,按进价增加 10%出售,后因库存积压降价,若按九折出售,则每件还能获利.( × )(2)函数 y=2x的函数值比 y=x2的函数值大.( × )(3)不存在 x0,使 ax01)的增长速度会超过并远远大于 y=xa(a>0)的增长速度.( √ )解析:(1)9 折出售的售价为 100(1+10%)×=99 元.∴每件赔 1 元,(1)错.(2)中,当 x=2 时,2x=x2=4.不正确.(3)中,如 a=x0=,n=,不等式成立,因此(3)错.2.小题热身(1)函数模型 y1=0.25x,y2=log2x+1,y3=1.002x,随着 x 的增大,增长速度的大小关系是 y3> y 1> y 2.(2)某车间分批生产某种产品,每批的生产准备费用为 800 元.若每批生产 x 件,则平均仓储时间为天,且每件产品每天的仓储费用为 1 元.把平均每件产品的生产准备费用与仓储费用之和 S 表示为 x 的函数是 S =+ ( x ∈ N * ) .(3)某物体一天中的温度 T 是关于时间 t 的函数,且 T=t3-3t+60,时间单位是小时,温度单位是℃,当 t=0 时表示中午 12:00,其后 t 值为正,则上午 8 时该物体的温度是 8_℃.(4)已知某种动物繁殖量 y(只)与时间 x(年)的关系为 y=alog3(x+1),设这种动物第 2 年有...