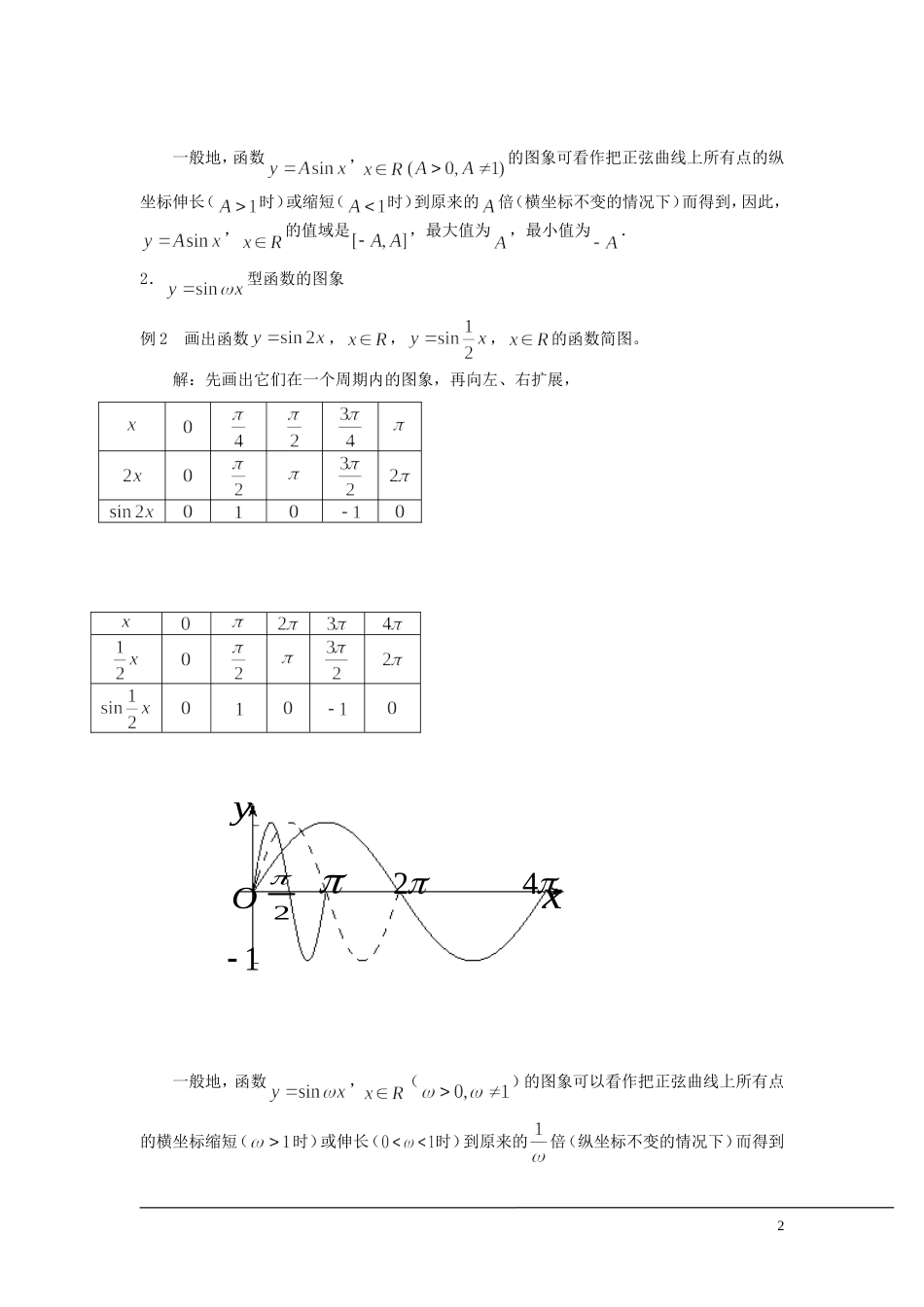
1.3.3 函数的图象(1)一、课题:函数的图象(1) 二、教学目标:1.会画函数的简图;2.弄清与函数的图象之间的关系;3.理解由简单到复杂,由特殊到一般的化归思想。三、教学重、难点:五点法画函数的图象。 四、教学过程:(一) 新课讲解:1.型函数的图象例 1 画出函数,,,,的简图。解:先画出它们在上的图象,再向左右扩展,由图可知,对于同一个,,的图象上的点的纵坐标等于,的图象上的点的纵坐标的倍,因此,,的图象可以看作正弦曲线上所有点的纵坐标伸长到原来的倍(横坐标不变的情况下)而得到的。,的图象的情况也类似:纵坐标变为原来的(横坐标不变情况下)。1xyO––32222sinyxsinyx1 sin2yx一般地,函数,的图象可看作把正弦曲线上所有点的纵坐标伸长(时)或缩短(时)到原来的倍(横坐标不变的情况下)而得到,因此,,的值域是,最大值为,最小值为.2.型函数的图象例 2 画出函数,,,的函数简图。解:先画出它们在一个周期内的图象,再向左、右扩展,一般地,函数,()的图象可以看作把正弦曲线上所有点的横坐标缩短(时)或伸长(时)到原来的倍(纵坐标不变的情况下)而得到2xyO2421––的。3.型的函数图象例 3 画出函数,,,的简图。解:由函数图象的平移知: ,的图象可看作,的图象向左平移个单位得到;,的图象可看作,的图象向右平移个单位得到。可得图象如下:一般地,函数(),的图象,可看作把正弦曲线上所有点向左(时)或向右(时)平行移动个单位而得到。五、课堂练习:画出下列函数在长度为一个周期的闭区间上的简图(五点法)。(1),; (2),.六、小结:1.型函数的图象; 2.型函数的图象;3.型函数的图象。七、作业:3xyO29453764354