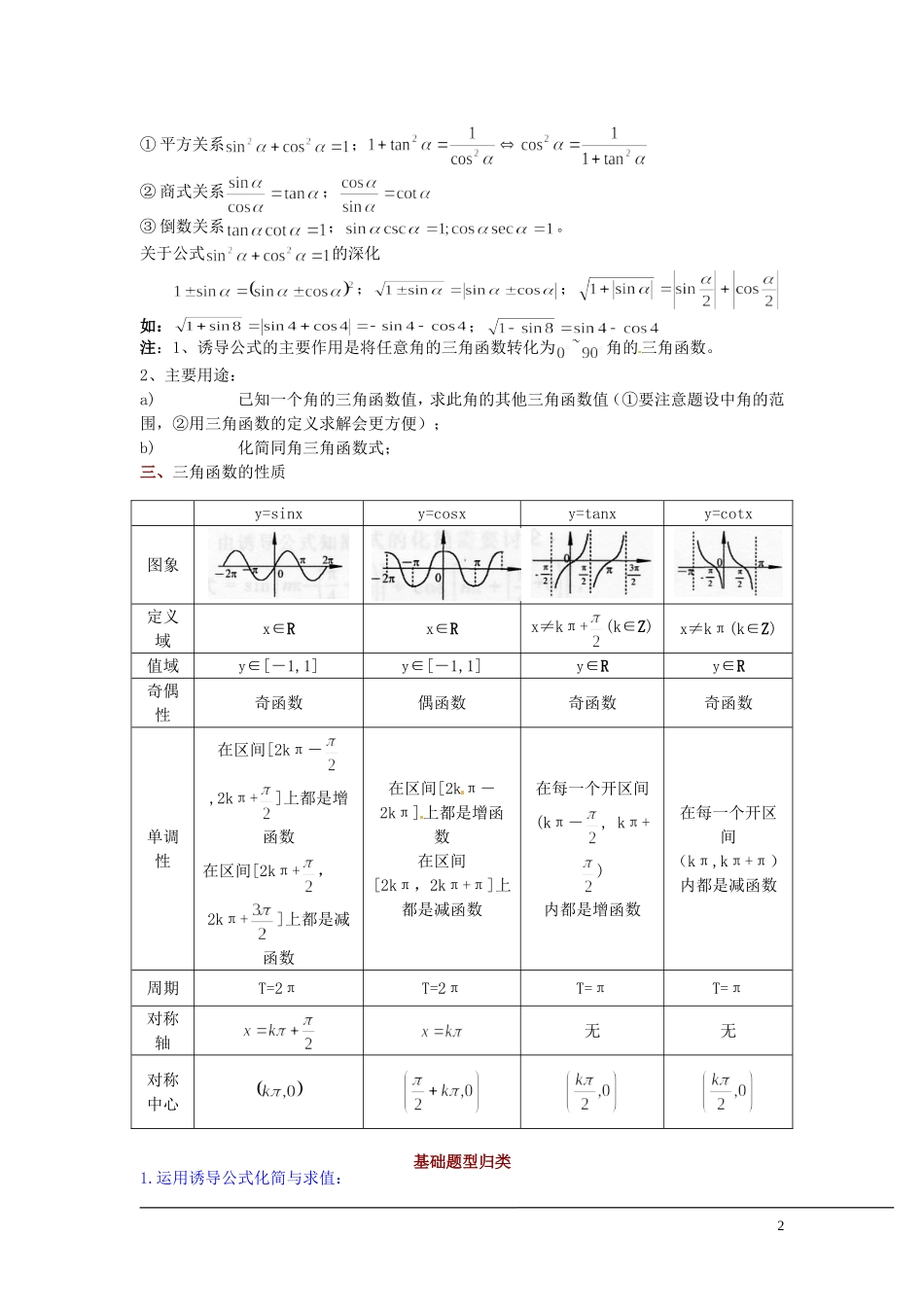
本章复习与小结三角函数一、三角函数的基本概念1.角的概念的推广(1)角的分类:正角(逆转) 负角(顺转) 零角(不转)(2)终边相同角:(3)直角坐标系中的象限角与坐标轴上的角.2.角的度量(1)角度制与弧度制的概念(2)换算关系:(3)弧长公式: 扇形面积公式: 3.任意角的三角函数注:三角函数值的符号规律“一正全、二正弦、三双切、四余弦”二、同角三角函数的关系式及诱导公式(一)诱导公式:tan与的 三 角 函 数 关 系 是 “ 立 变 平 不 变 , 符 号 看 象 限 ” 。 如 :等。(二)同角三角函数的基本关系式:1① 平方关系;② 商式关系;③ 倒数关系;。关于公式的深化;;如:;注:1、诱导公式的主要作用是将任意角的三角函数转化为~角的三角函数。2、主要用途:a)已知一个角的三角函数值,求此角的其他三角函数值(①要注意题设中角的范围,②用三角函数的定义求解会更方便);b)化简同角三角函数式;三、三角函数的性质y=sinxy=cosxy=tanxy=cotx图象定义域x∈Rx∈Rx≠kπ+(k∈Z)x≠kπ(k∈Z)值域y∈[-1,1]y∈[-1,1]y∈Ry∈R奇偶性奇函数偶函数奇函数奇函数单调性在区间[2kπ-,2kπ+]上都是增函数在区间[2kπ+,2kπ+]上都是减函数在区间[2kπ-2kπ]上都是增函数在区间[2kπ,2kπ+π]上都是减函数在每一个开区间(kπ-, kπ+)内都是增函数在每一个开区间(kπ,kπ+π)内都是减函数周期T=2πT=2πT=πT=π对称轴无无对称中心 基础题型归类1.运用诱导公式化简与求值:2要求:掌握,,,,,等诱导公式. 记忆口诀:奇变偶不变,符号看象限.例 1.求值:练 1 (1)若 cos(π+α)=,<α<2π, 则 sin(2π-α)等于 .(2)若,那么的值为 .(3)(π)的值为 .2.运用同角关系化简与求值:要求:掌握同角二式(,),并能灵活运用. 方法:平方法、切弦互化.例 2 (1)化简; (2)已知, 且, 求的值.练 2 (1)已知,且<α<,则的值为 .(2)已知=3, 计算:(i); (ii).3.运用单位圆及三角函数线:要求:掌握三角函数线,利用它解简单的三角方程与三角不等式. 方法:数形结合.例 5 (1)已知,则、、的大小顺序为 .(2)函数的定义域为 .练 5 (1)若, 则角 α 的取值集合为____________.(2)在区间(0,2)内,使成立的 的取值范围 .4.弧度制与扇形弧长、面积公式:要求:掌握扇形的弧长与面积计算公式,掌握弧度制. 方法:方程思想.例 6 某扇形的面积为 1,它的周长为 4,那么该...