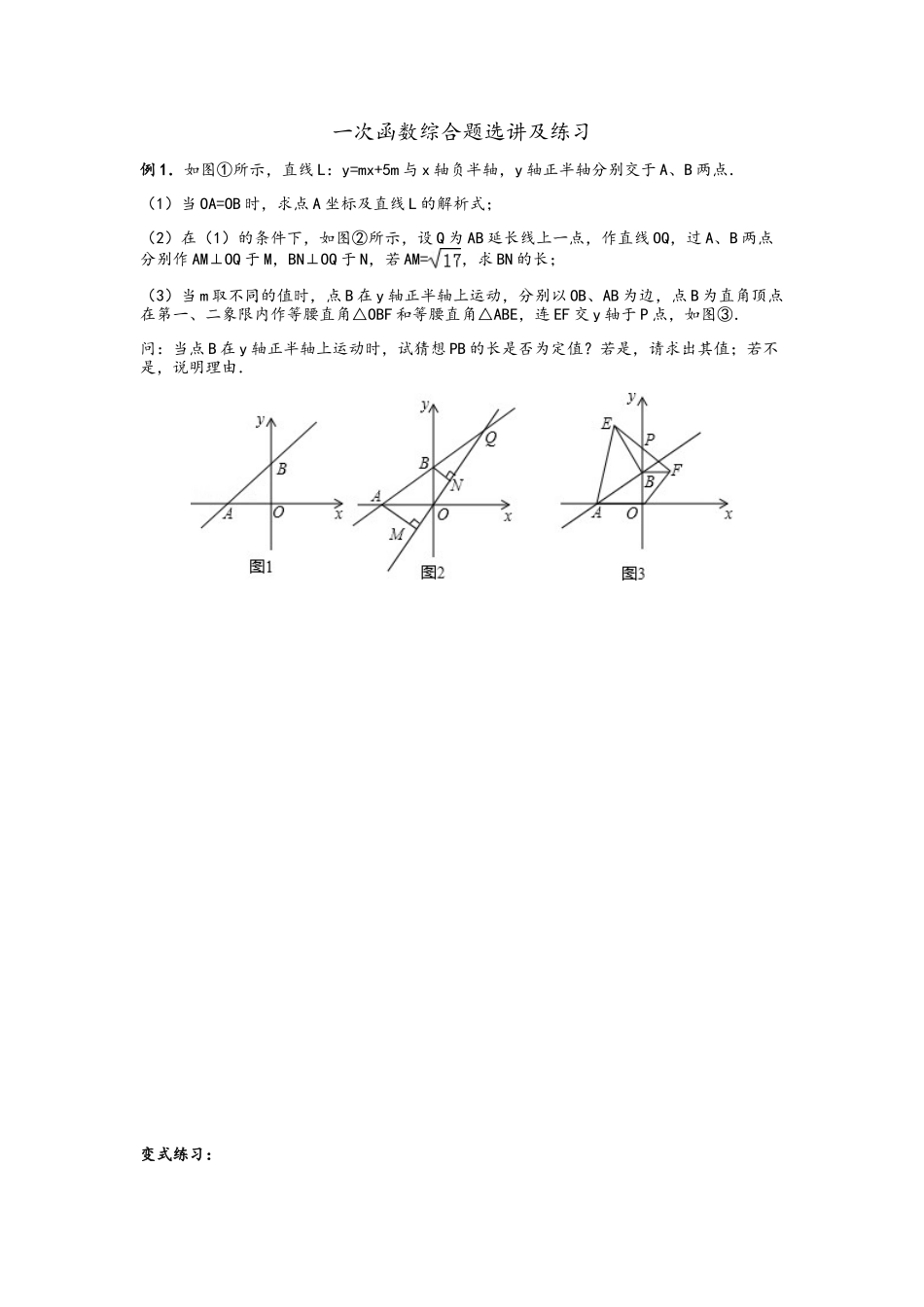
一次函数综合题选讲及练习例 1.如图①所示,直线 L:y=mx+5m 与 x 轴负半轴,y 轴正半轴分别交于 A、B 两点.(1)当 OA=OB 时,求点 A 坐标及直线 L 的解析式;(2)在(1)的条件下,如图②所示,设 Q 为 AB 延长线上一点,作直线 OQ,过 A、B 两点分别作 AM⊥OQ 于 M,BN⊥OQ 于 N,若 AM=,求 BN 的长;(3)当 m 取不同的值时,点 B 在 y 轴正半轴上运动,分别以 OB、AB 为边,点 B 为直角顶点在第一、二象限内作等腰直角△OBF 和等腰直角△ABE,连 EF 交 y 轴于 P 点,如图③.问:当点 B 在 y 轴正半轴上运动时,试猜想 PB 的长是否为定值?若是,请求出其值;若不是,说明理由.变式练习:1.已知:如图 1,一次函数 y=mx+5m 的图象与 x 轴、y 轴分别交于点 A、B,与函数 y=﹣ x的图象交于点 C,点 C 的横坐标为﹣3.(1)求点 B 的坐标;(2)若点 Q 为直线 OC 上一点,且 S△QAC=3S△AOC,求点 Q 的坐标;(3)如图 2,点 D 为线段 OA 上一点,∠ACD=∠AOC.点 P 为 x 轴负半轴上一点,且点 P 到直线 CD 和直线 CO 的距离相等.① 在图 2 中,只利用圆规作图找到点 P 的位置;(保留作图痕迹,不得在图 2 中作无关元素.)② 求点 P 的坐标.例 2.如图 1,已知一次函数 y=﹣ x+6 分别与 x、y 轴交于 A、B 两点,过点 B 的直线 BC 交x 轴负半轴与点 C,且 OC= OB.(1)求直线 BC 的函数表达式;(2)如图 2,若△ABC 中,∠ACB 的平分线 CF 与∠BAE 的平分线 AF 相交于点 F,求证:∠AFC= ∠ABC;(3)在 x 轴上是否存在点 P,使△ABP 为等腰三角形?若存在,请直接写出 P 点的坐标;若不存在,请说明理由.变式练习:2.如图,直线 l:y= x+6 交 x、y 轴分别为 A、B 两点,C 点与 A 点关于 y 轴对称.动点P、Q 分别在线段 AC、AB 上(点 P 不与点 A、C 重合),满足∠BPQ=∠BAO.(1)点 A 坐标是 ,BC= .(2)当点 P 在什么位置时,△APQ≌△CBP,说明理由.(3)当△PQB 为等腰三角形时,求点 P 的坐标.课后作业:1.已知,如图直线 y=2x+3 与直线 y=﹣2x﹣1 相交于 C 点,并且与两坐标轴分别交于 A、B两点.(1)求两直线与 y 轴交点 A,B 的坐标及交点 C 的坐标;(2)求△ABC 的面积.2.如图①,直线 y=﹣ x+1 分别与坐标轴交于 A,B...