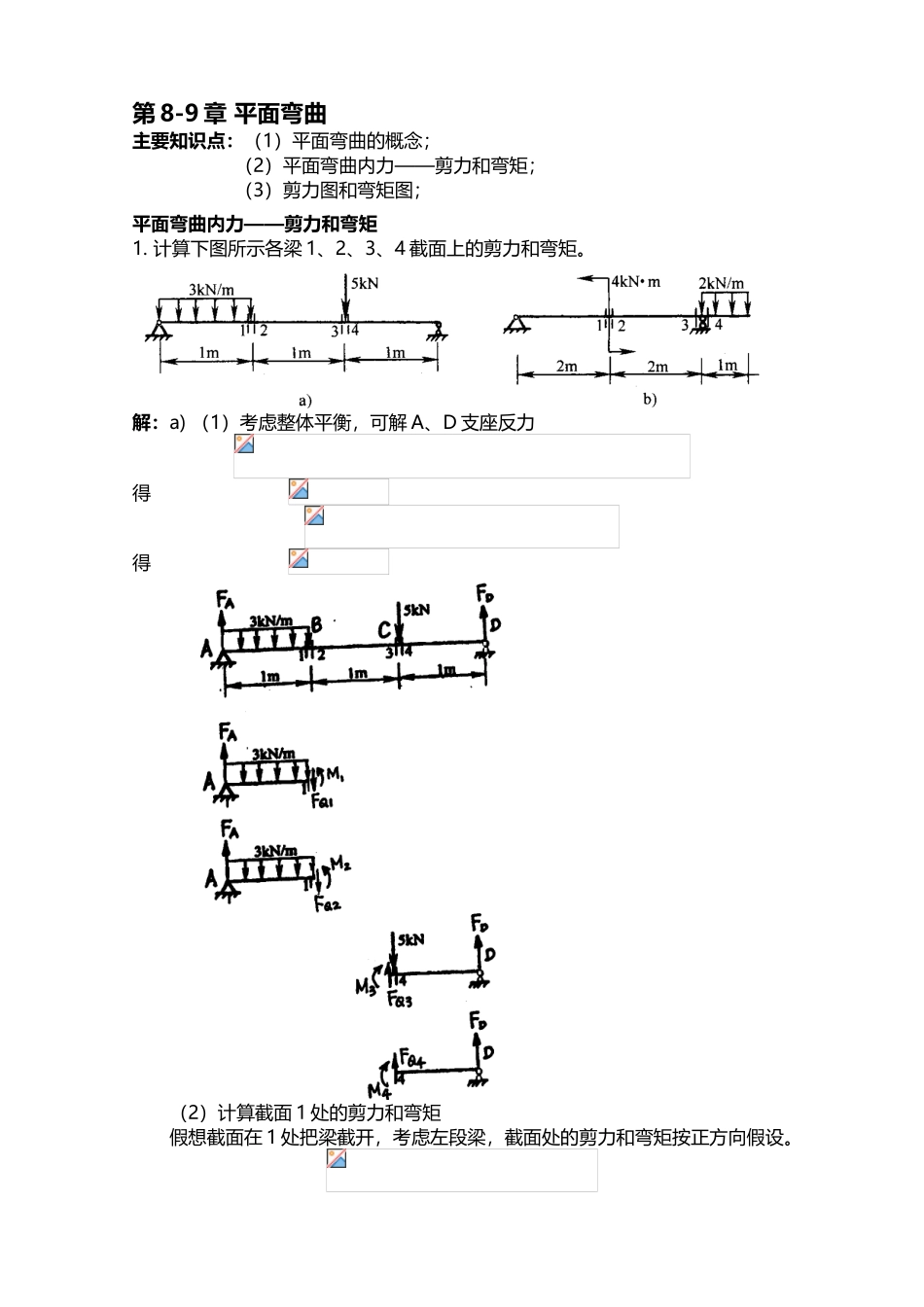
平面弯曲习题解答 1(9 页)Good is good, but better carries it.精益求精,善益求善。第 8-9 章 平面弯曲主要知识点:(1)平面弯曲的概念;(2)平面弯曲内力——剪力和弯矩;(3)剪力图和弯矩图;平面弯曲内力——剪力和弯矩1. 计算下图所示各梁 1、2、3、4 截面上的剪力和弯矩。解:a) (1)考虑整体平衡,可解 A、D 支座反力得 得 (2)计算截面 1 处的剪力和弯矩假想截面在 1 处把梁截开,考虑左段梁,截面处的剪力和弯矩按正方向假设。得 得 (3) 计算截面 2 处的剪力和弯矩假想截面 2 在处把梁截开,考虑左段梁,截面处的剪力和弯矩按正方向假设。得 得 (4) 计算截面 3 处的剪力和弯矩假想截面在 3 处把梁截开,考虑右段梁,截面处的剪力和弯矩按正方向假设。得 得 (5) 计算截面 4 处的剪力和弯矩假想截面在 4 处把梁截开,考虑右段梁,截面处的剪力和弯矩按正方向假设。得 得 将上述结果列表如下:截面1234剪力(kN)1.171.171.17-3.83弯矩()2.672.673.833.83b) (1)考虑整体平衡,可解 A、C 支座反力得 得 (2)计算截面 1 处的剪力和弯矩假想截面在 1 处把梁截开,考虑左段梁,截面处的剪力和弯矩按正方向假设。得 得 (3) 计算截面 2 处的剪力和弯矩假想截面 2 在处把梁截开,考虑左段梁,截面处的剪力和弯矩按正方向假设。得 得 (4) 计算截面 3 处的剪力和弯矩假想截面在 3 处把梁截开,考虑右段梁,截面处的剪力和弯矩按正方向假设。得 得 (5) 计算截面 4 处的剪力和弯矩假想截面在 4 处把梁截开,考虑右段梁,截面处的剪力和弯矩按正方向假设。得 得 将上述结果列表如下:截面1234剪力(kN)0.750.750.752弯矩()1.5-2.5-1-1剪力图和弯矩图2. 建立图示梁的剪力方程和弯矩方程,并画剪力图和弯矩图。 (a)(b)解:a)(1)求支座反力(2)求剪力方程和弯矩方程(分段建立方程) AC 段 CB 段(3)作剪力图和弯矩图 弯矩图是两斜直线,在 C 截面处有突变,突变量为 M。b) (1)求支座反力由整体平衡方程(见图 8-2b): , , , , (2)求剪力方程和弯矩方程 梁上任取一截面(见图 8-2b),到支座 A 的距离为 x,由截面法得该截面的剪力方程和弯矩方程AB 段:,,()BC 段: , ,即,()图 8-2b(3)作剪力图和弯矩图:AB、BC 段剪力都为常数,剪力图各为一水平直线。AB、BC 段弯矩方程是 x 的一次函数,弯矩图各为...