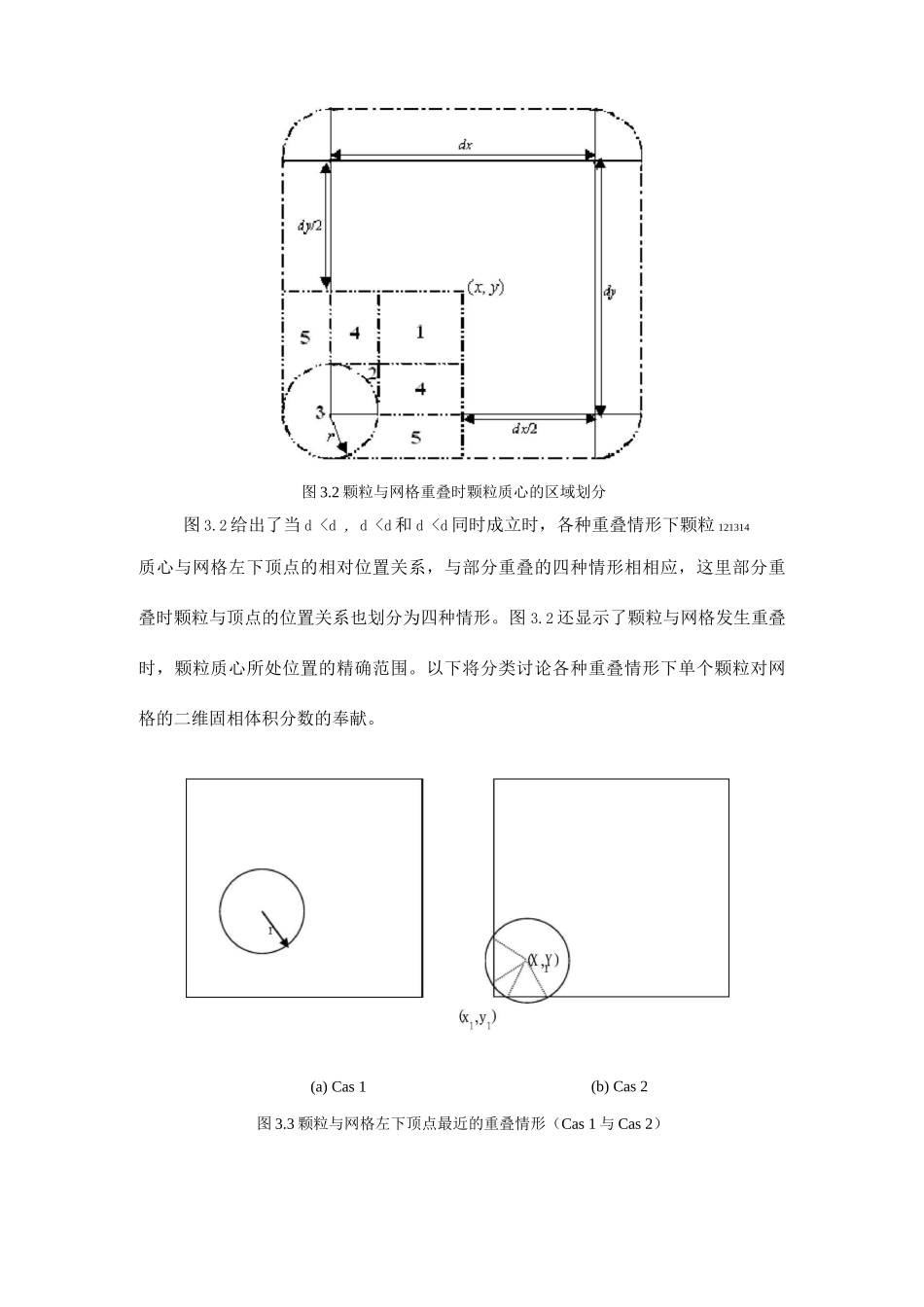
精确二维固相体积分率方案为了精确计算二维固相体积分数,将颗粒与网格的部分重叠进一步细分为四种情形。图 3. 1 中给出了各种重叠情形下颗粒与网格的相对位置关系示意。计算网格的二维固相体积分数时,部分重叠的四种情形还需要进一步区分网格顶点与颗粒的位置关系。本章模拟采纳正方形网格进行空间离散,这里令颗粒的坐标为(X ,Y),网格宽度和厚度分别为 dx, dy ,网格的几何中心为(x, y),网格的四个顶点分别为(x dx/2, y dy /2) , (x dx/2, y dy /2) , (x dx/2, y dy/2)和(x dx/2,y dy /2),由此可计算颗粒与四个顶点的距离"叫叫和这些距离中,当 di,d2,d3和 d]分别为最小时,单颗粒所占网格的二维固相体积分数的表达形式存在差别,不失一般性,这里只给出当 d r。尽管情形 3 存在四种变例,但通过推导,颗粒所占网格的二维固相体积分数的表达形式是统一的。根据图 3.4 容易得到则颗粒 i 所占目的网格的二维固相体积分数为°1 12r2 a2 b2 1 而f - r2 arccos -a Yi x y 22r22图 3.3 给出了颗粒与网格左下顶点距离最近的重叠情形 1 和 2。这两种情形下,颗粒所占网格的二维固相体积分数的表达形式是唯一拟定的,不存在变例。对于情形 1,颗粒质心与网格的位置关系为:x1 r X 乂且七Y y。则单个满足重叠情形 1 的颗粒浙占目的网格的二维固相体积分数为fr2i x y(3.3)对于情形 2,颗粒质心与网格的位置关系为:x1y1y1P 1— X x Y y 1Xf ----- r2 r...