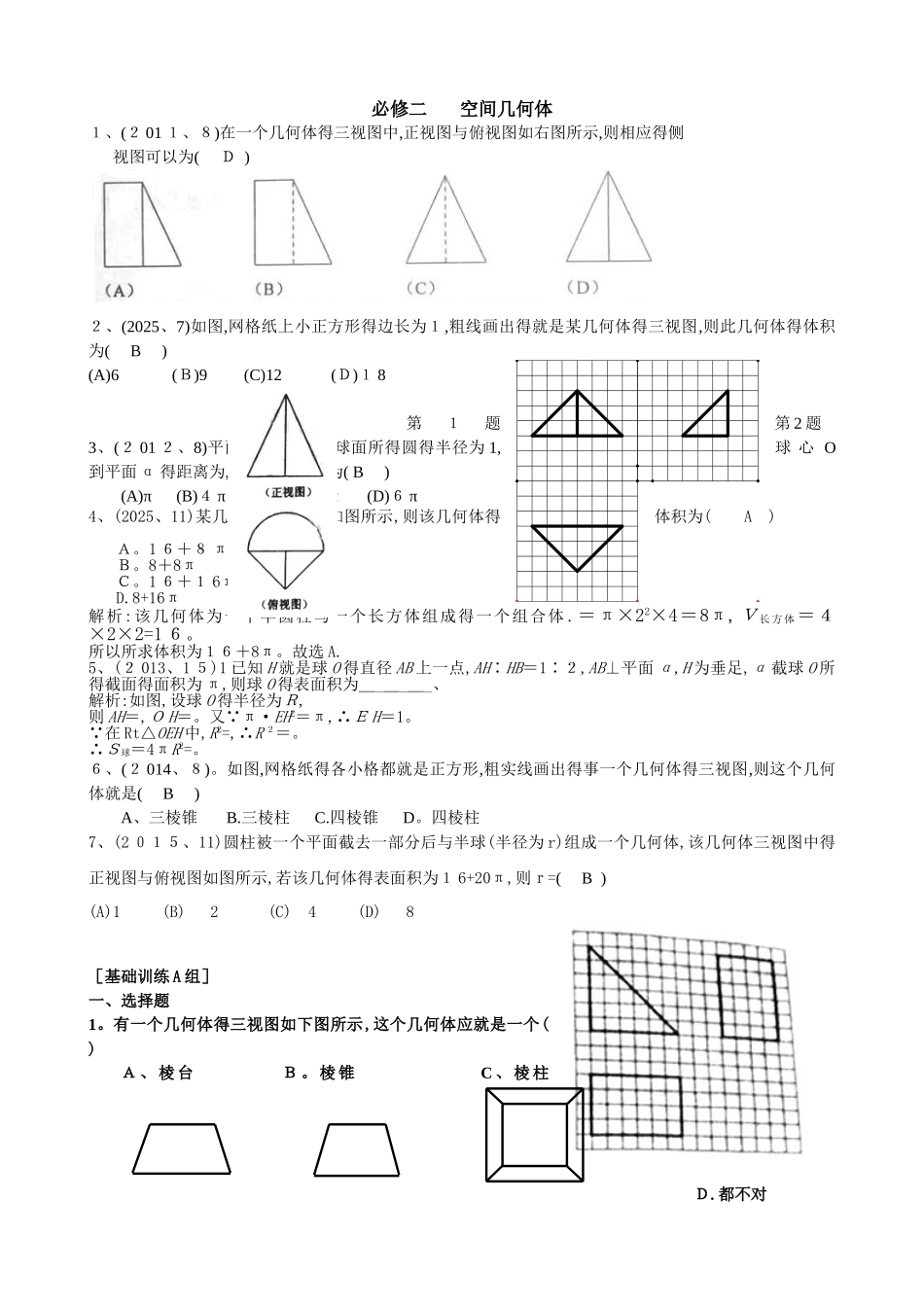
必修二 空间几何体1、(2 01 1、8)在一个几何体得三视图中,正视图与俯视图如右图所示,则相应得侧视图可以为( D )2、(2025、7)如图,网格纸上小正方形得边长为1,粗线画出得就是某几何体得三视图,则此几何体得体积为( B )(A)6 (B)9 (C)12 (D)1 8 第1题 第 2 题3、(2 01 2、8)平面 α 截球 O 得球面所得圆得半径为 1,球 心 O到平面 α 得距离为,则此球得体积为( B ) (A)π (B)4 π (C)4π (D)6 π4、(2025、11)某几何体得三视图如图所示,则该几何体得体积为( A )A。1 6+8 π B。8+8πC。1 6+1 6π D.8+16π解析:该几何体为一个半圆柱与一个长方体组成得一个组合体 .=π×22×4=8π,V 长方体=4×2×2=1 6。所以所求体积为16+8π。故选 A.5、(2 013、1 5)1 已知 H 就是球 O 得直径 AB 上一点,AH∶HB=1∶2,AB⊥平面 α,H 为垂足,α 截球 O 所得截面得面积为 π,则球 O 得表面积为______、解析:如图,设球 O 得半径为R,则 AH=,O H=。又 π·EH2=π,∴E H=1。 在 Rt△OEH 中,R2=,∴R 2=。 ∴S球=4πR2=。6、(2 014、8)。如图,网格纸得各小格都就是正方形,粗实线画出得事一个几何体得三视图,则这个几何体就是( B )A、三棱锥 B.三棱柱 C.四棱锥 D。四棱柱7、(2 015、11)圆柱被一个平面截去一部分后与半球(半径为 r)组成一个几何体,该几何体三视图中得正视图与俯视图如图所示,若该几何体得表面积为1 6+20π,则r=( B ) (A)1 (B) 2 (C) 4 (D) 8[基础训练 A 组]一、选择题1。有一个几何体得三视图如下图所示,这个几何体应就是一个( )A 、 棱 台 B 。 棱 锥 C 、 棱 柱 D.都不对解:从俯视图来瞧,上、下底面都就是正方形,但就是大小不一样,可以推断就是棱台2、棱长都就是得三棱锥得表面积为( )A。 B. C、 D、 解:因为四个面就是全等得正三角形,则3.长方体得一个顶点上三条棱长分别就是,且它得个顶点都在同一球面上,则这个球得表面积就是( ) A、 B. C. D、都不对解:长方体得对角线就是球得直径,4、正方体得内切球与外接球得半径之比为( )A、 B、 C. D。解:正方体得棱长就是内切球得直径,正方体得对角线就是外接球得直径,设棱长就是 5.在△A BC 中,,若使绕直线旋转一周,则所形成得几何体得体积就是( )A。 B. C. D. 解:6。底面就是菱形得棱柱其侧棱垂直于...