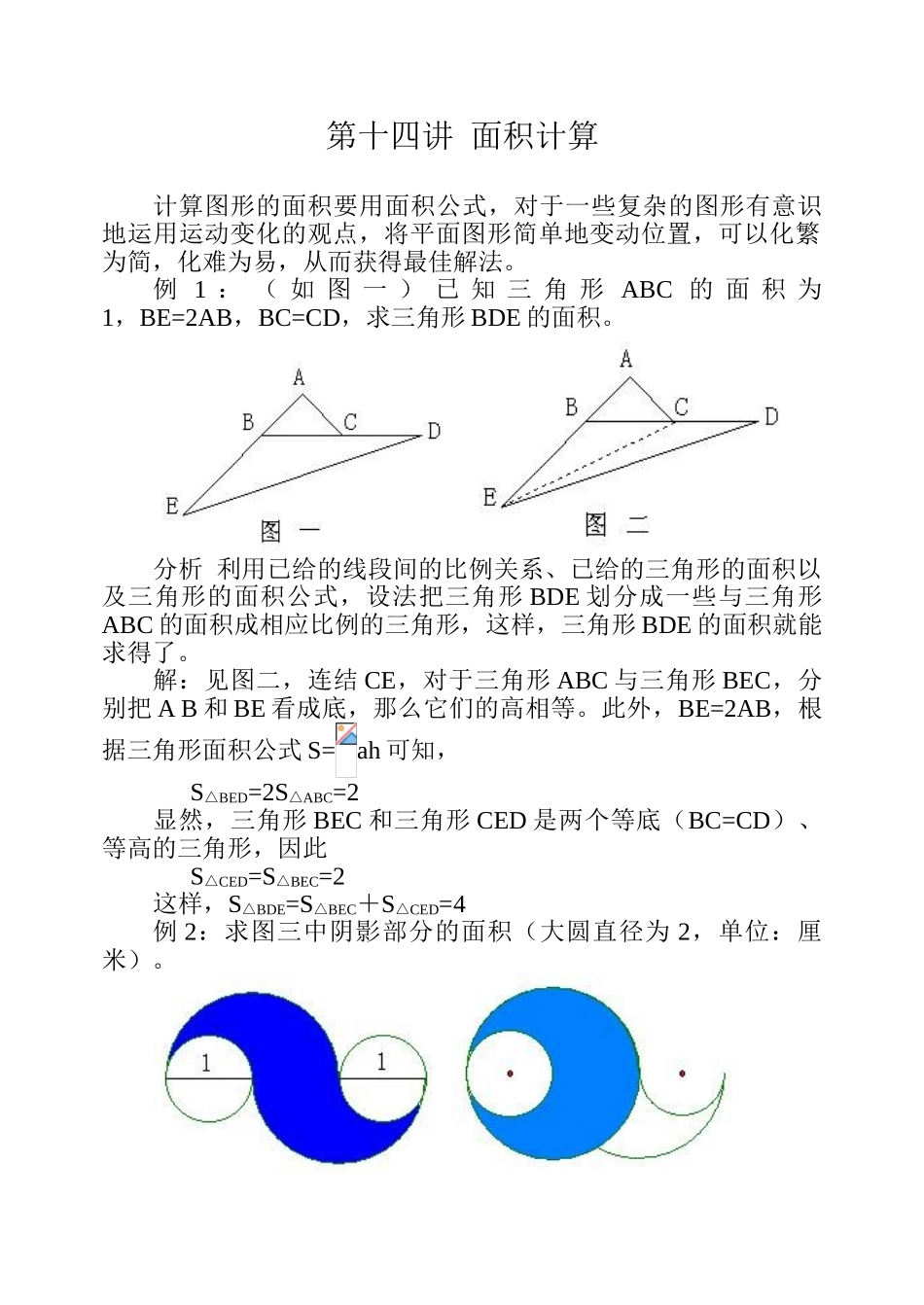
第十四讲 面积计算计算图形的面积要用面积公式,对于一些复杂的图形有意识地运用运动变化的观点,将平面图形简单地变动位置,可以化繁为简,化难为易,从而获得最佳解法。例 1 : ( 如 图 一 ) 已 知 三 角 形 ABC 的 面 积 为1,BE=2AB,BC=CD,求三角形 BDE 的面积。 分析 利用已给的线段间的比例关系、已给的三角形的面积以及三角形的面积公式,设法把三角形 BDE 划分成一些与三角形ABC 的面积成相应比例的三角形,这样,三角形 BDE 的面积就能求得了。解:见图二,连结 CE,对于三角形 ABC 与三角形 BEC,分别把 A B 和 BE 看成底,那么它们的高相等。此外,BE=2AB,根据三角形面积公式 S=ah 可知, S△BED=2S△ABC=2显然,三角形 BEC 和三角形 CED 是两个等底(BC=CD)、等高的三角形,因此 S△CED=S△BEC=2这样,S△BDE=S△BEC+S△CED=4例 2:求图三中阴影部分的面积(大圆直径为 2,单位:厘米)。 图 三 图 四分析 解题时可以先将图形下半部分翻转拼接为图四,然后将图中的小圆移至中心。从图中不难看出求原图中阴影部分的面积就是求一个圆环的面积。解:大圆半径:2÷2=1(厘米) 小圆半径:1÷2=0.5(厘米) 阴影面积:3.14×(12-0.52)=2.355(平方厘米)答:阴影部分的面积是 2.355 平方厘米。例 3:如下图,在图中三角形 ABE、ADF 和四边形 AECF 的面积相等,求三角形 AEF 的面积。分析 三角形 AEF 的面积等于四边形 AECF 的面积减去三角形 ECF 的面积,因为长方形 ABCD 的面积等于三角形 ABE、ADF和四边形 AECF 的面积和,而这三者的面积又相等,所以四边形AECF 的面积等于长方形面积的。由于长方形 ABCD 的长、宽分别为 9 厘米和 6 厘米,因此很容易求出它的面积,所以解题的关键在于求出三角形 ECF 的面积。根据三角形面积公式 S=ah,已知三角形 ABE 的面积等于长方形面积的,又知道 AB=6 厘米,可以求出 BE 的长度。知道BE 的长度就可以求出 EC 的长度。同理可以求出 FC 的长度。这样三角形 ECF 的面积可以求出,使问题得解。解:长方形 ABCD 的面积:9×6=54(平方厘米)四边形 AECF 及三角形 ABE、AFD 的面积相等,是: 54× =18(平方厘米);EC 的长度:9-18×2÷6=3(厘米)FC 的长度:6-18×2÷9=2(厘米)三角形 AEF 的面积:18-3×2÷2=15(平方厘米)。答:三角形 AEF 的面积是 15 平方厘米。...