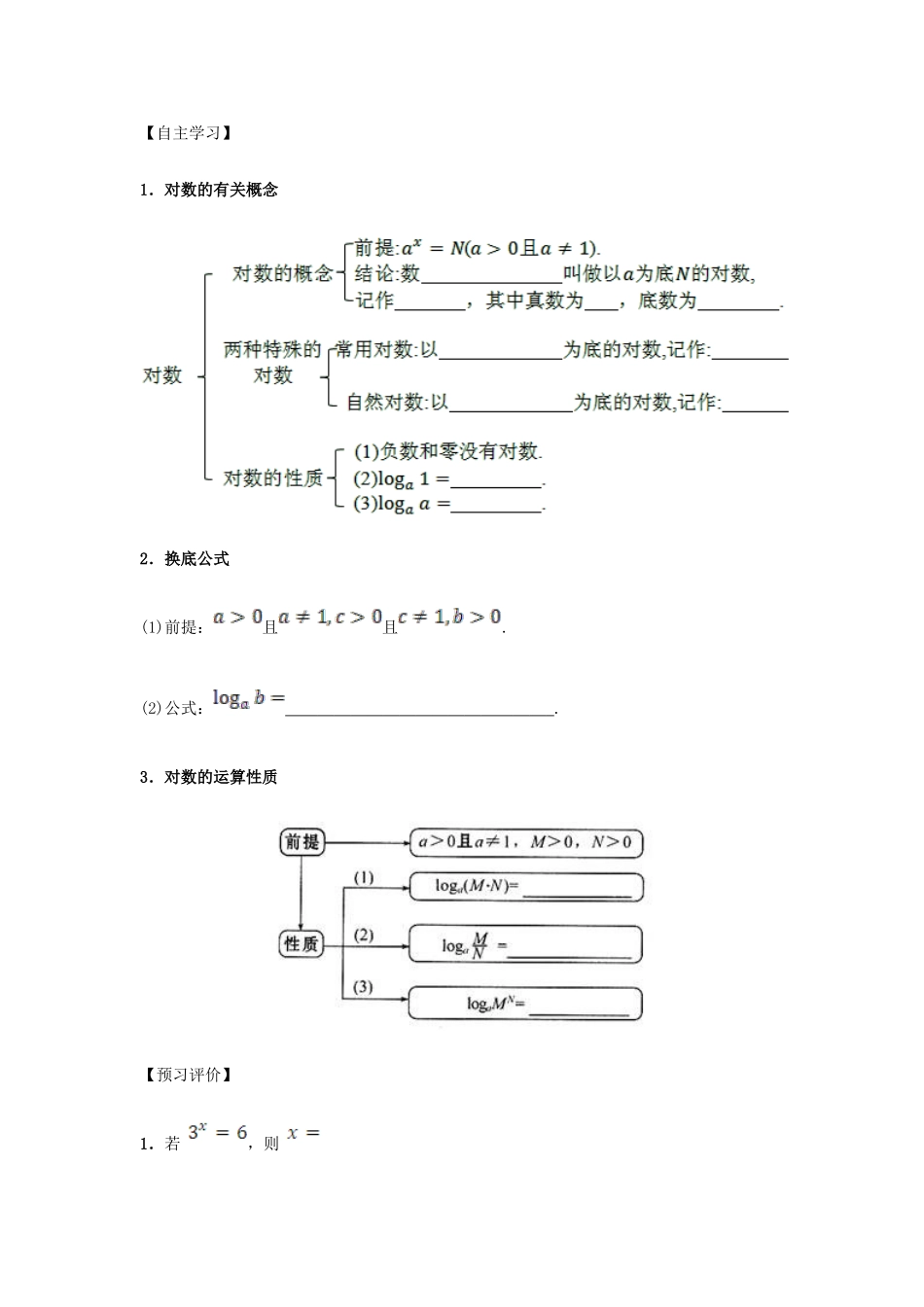
2.2.1 对数与对数运算班级:__________姓名:__________设计人__________日期__________课前预习 · 预习案【温馨寄语】你的天赋好比一朵火花,假如你用勤勉辛劳去助燃,它一定会变成熊熊烈火,放出无比的光和热来。【学习目标】1.理解对数的概念,掌握常用对数及自然对数.2.熟记并能够运用对数的性质进行计算或化简.3.能够熟练地进行指数式与对数式的互化.4.掌握对数的运算性质,并能运用运算性质进行对数的有关运算.5.了解换底公式并能用换底公式将一般对数化成自然对数和常用对数.【学习重点】1.指数式与对数式的互化2.对数的运算性质3.换底公式的应用【学习难点】1.对数概念的理解2.对数的运算性质的应用3.对数的换底公式推导及换底公式的逆用【自主学习】1.对数的有关概念2.换底公式(1)前提:且且.(2)公式: .3.对数的运算性质【预习评价】1.若 ,则 A. B. C. D. 2.A.0 B.1 C.2 D.33.A.4 B.3 C.2 D.14.在对数式 中,真数是 ,底数是 .5.计算 , .6.将 化为对数式为 .7.若且,则下列等式正确的是A.B.C.D.8.计算:A.3 B.2 C.1 D.09.A.1 B.2 C.3 D.410.若且,则 .11.已知,那么 .知识拓展 · 探究案【合作探究】1.对数的概念及其与指数式的互化 根据对数的概念及其与指数式的互化关系式 根据对数式中底数 的取值范围,回答下列问题:(1)对数的底数 可以等于 0 或 1 吗?(2)当对数的底数 时,对数式是否成立?2.对数的概念及其与指数式的互化 根据对数的概念及其与指数式的互化关系式 结合指数式与对数式的互化完成下列问题,明确指数式与对数式之间的关系:(l)在表格的空白处填写 , , 这三个字母的名称.(2)任何一个指数式都可以化成对数式呜?3.对数的性质及对数恒等式 通过下列问题的探究,明确对数具有的性质.(l)在对数式 ( )中只有 ,才有意义,思考为什么负数和零没有对数?(2)试利用所学的知识解释对数式 与 为什么成立?4.对数的性质及对数恒等式 完成下列几个问题,认识对数恒等式及其具有的特点.(1)若 且 ,由 可知, .把 代人 可得什么结论,它的意义如何?举例说明.(2)在探究(1)所得结论的基础上,试化简式子 ,结果如何?(3)结合探究(2)说明利用公式 ( 且 )化简求值的关键是什么?5.对数的运算性质 运算性质中底数 能等于零或小于零吗,真数呢?6.对数的运算性质 对数的运算性质(1)能否推广为,试证明.7.换底公式观察换底公式,思考下...