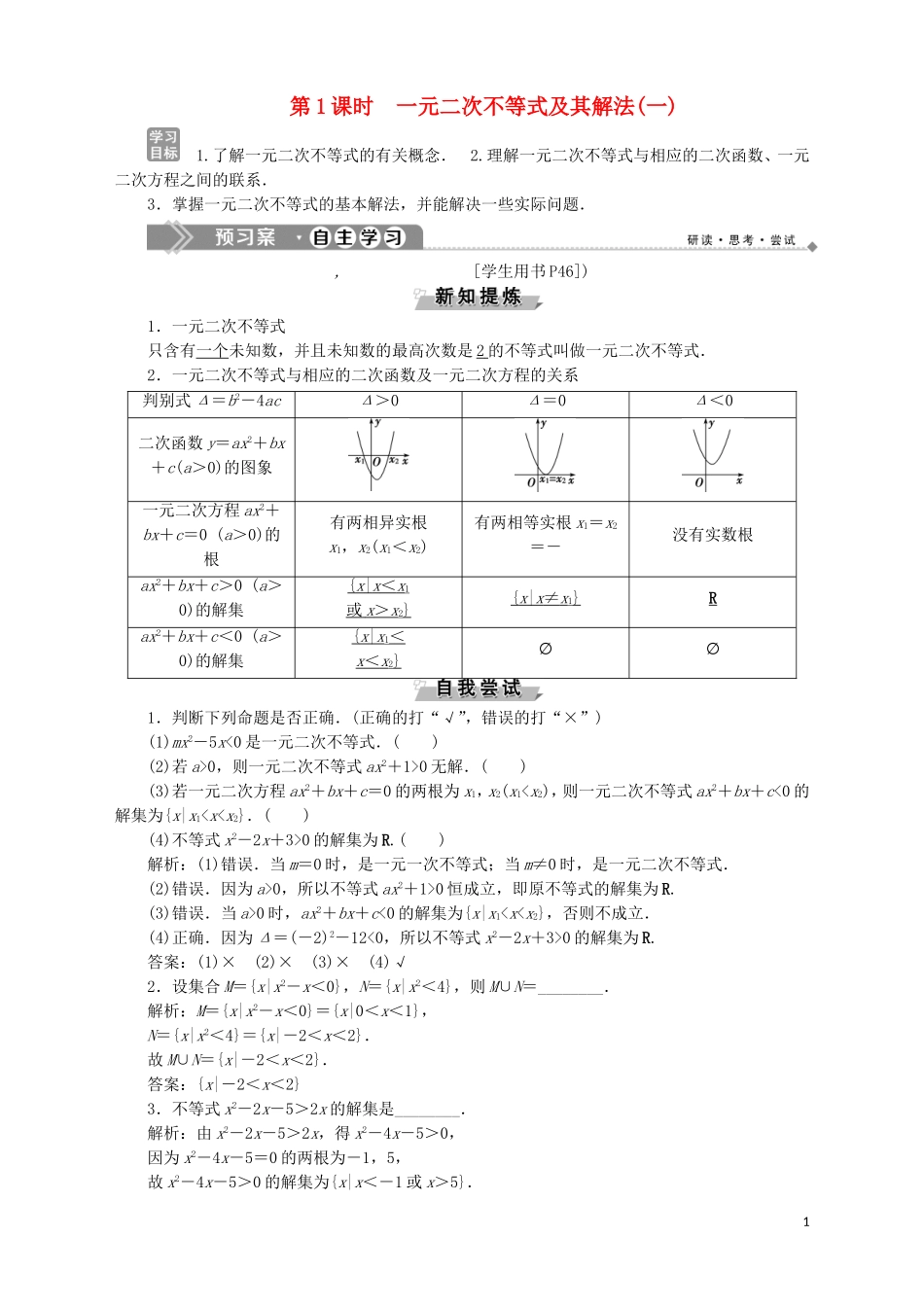
第 1 课时 一元二次不等式及其解法(一) 1.了解一元二次不等式的有关概念. 2.理解一元二次不等式与相应的二次函数、一元二次方程之间的联系.3.掌握一元二次不等式的基本解法,并能解决一些实际问题., [学生用书 P46])1.一元二次不等式只含有一个未知数,并且未知数的最高次数是 2 的不等式叫做一元二次不等式.2.一元二次不等式与相应的二次函数及一元二次方程的关系判别式 Δ=b2-4acΔ>0Δ=0Δ<0二次函数 y=ax2+bx+c(a>0)的图象一元二次方程 ax2+bx+c=0 (a>0)的根有两相异实根x1,x2(x1<x2)有两相等实根 x1=x2=-没有实数根ax2+bx+c>0 (a>0)的解集{ x | x < x 1或 x > x 2}{ x | x ≠ x 1}Rax2+bx+c<0 (a>0)的解集{ x | x 1<x < x 2}∅∅1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)(1)mx2-5x<0 是一元二次不等式.( )(2)若 a>0,则一元二次不等式 ax2+1>0 无解.( )(3)若一元二次方程 ax2+bx+c=0 的两根为 x1,x2(x10 的解集为 R.( )解析:(1)错误.当 m=0 时,是一元一次不等式;当 m≠0 时,是一元二次不等式.(2)错误.因为 a>0,所以不等式 ax2+1>0 恒成立,即原不等式的解集为 R.(3)错误.当 a>0 时,ax2+bx+c<0 的解集为{x|x10 的解集为 R.答案:(1)× (2)× (3)× (4)√2.设集合 M={x|x2-x<0},N={x|x2<4},则 M∪N=________.解析:M={x|x2-x<0}={x|0<x<1},N={x|x2<4}={x|-2<x<2}.故 M∪N={x|-2<x<2}.答案:{x|-2<x<2}3.不等式 x2-2x-5>2x 的解集是________.解析:由 x2-2x-5>2x,得 x2-4x-5>0,因为 x2-4x-5=0 的两根为-1,5,故 x2-4x-5>0 的解集为{x|x<-1 或 x>5}.1答案:{x|x>5 或 x<-1}4.不等式-3x2+5x-4>0 的解集为________.解析:原不等式变形为 3x2-5x+4<0.因为 Δ=(-5)2-4×3×4=-23<0,所以 3x2-5x+4=0 无解.由函数 y=3x2-5x+4 的图象可知,3x2-5x+4<0 的解集为∅.答案:∅ 解不含参数的一元二次不等式[学生用书 P46] 解下列不等式.(1)2x2+5x-3<0;(2)-3x2+6x≤2;(3)4x2-4x+1>0;(4)-x2+6x-10>0.【...