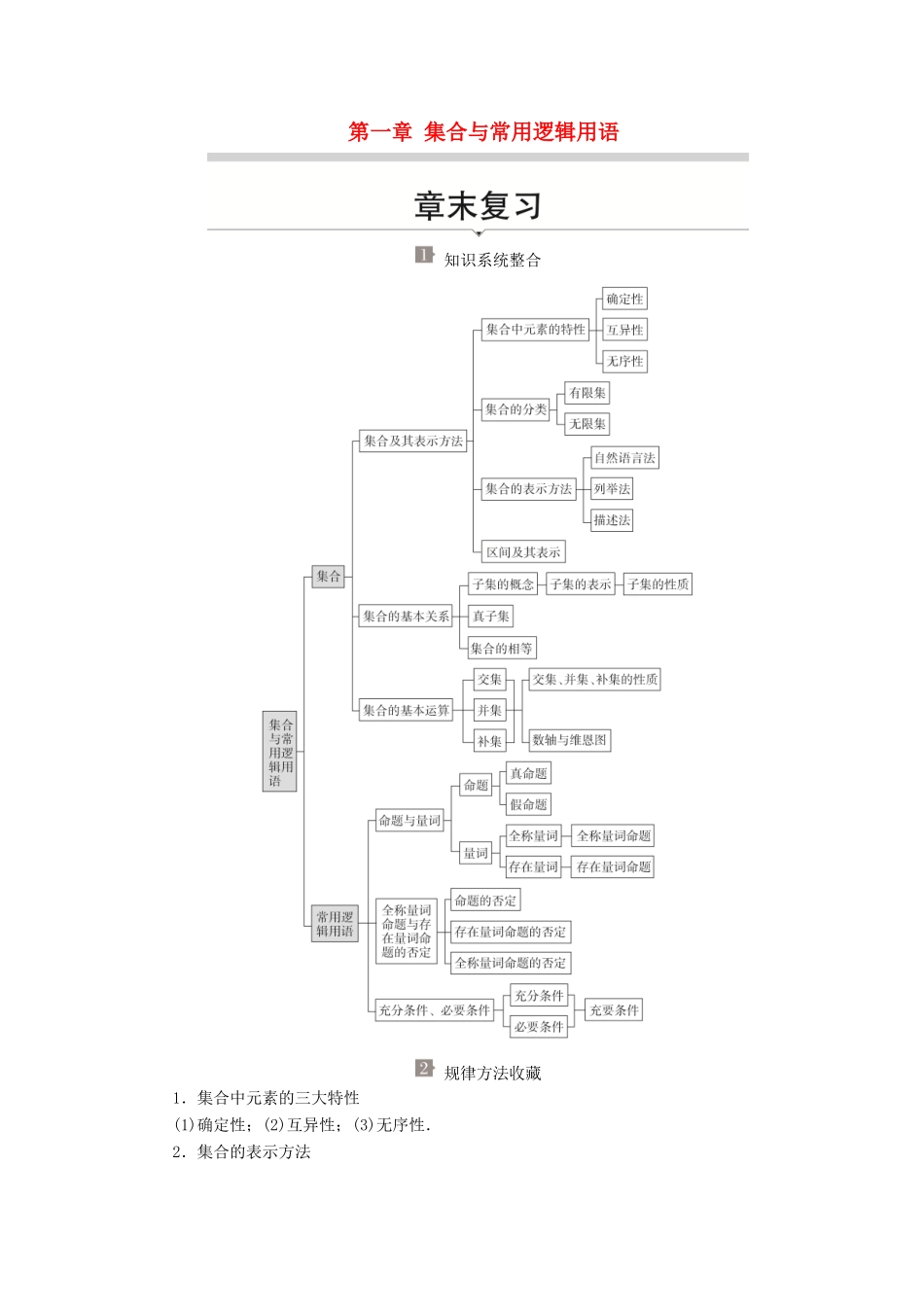
第一章 集合与常用逻辑用语 知识系统整合 规律方法收藏1.集合中元素的三大特性(1)确定性;(2)互异性;(3)无序性.2.集合的表示方法集合的表示方法的适用条件:(1)列举法:是对有限集且在元素不太多的情况下或元素个数较多且成一定规律时采用的,元素之间用“,”分隔开.(2)描述法:注意集合的代表元素及元素具备的性质.3.集合间的关系处理集合间的关系时需要注意:(1)涉及某些数集是不等式的解集时,利用数轴可较好地处理一些实数集之间的关系;(2)注意应用 B⊆A 的条件时,一定要考虑 B=∅和 B≠∅两种情况;(3)以形助数,直观形象,充分利用数形结合思想,同时注意转化思想,等价变形思想的灵活运用.4.子集、全集、补集的概念及交集、并集、补集运算的性质子集、全集、补集的概念实质上是生活中的“部分”“全体”“剩余”的概念在数学中的抽象与反应.(1)交集运算的性质A∩A=A;A∩∅=∅;A∩B=B∩A;(A∩B)∩C=A∩(B∩C);如果 A⊆B,则 A∩B=A.(2)并集运算的性质A∪A=A;A∪∅=A;A∪B=B∪A;(A∪B)∪C=A∪(B∪C);如果 A⊆B,则 A∪B=B.(3)补集运算的性质∁U(∁UA)=A;A∩(∁UA)=∅;∁U(A∩B)=(∁UA)∪(∁UB);∁U(A∪B)=(∁UA)∩(∁UB).5.命题(1)判断一个语句是不是命题就是要看它是否符合是“陈述句”和“可以判断真假”这两个条件,只有同时满足这两个条件的才是命题.(2)一个命题要么是真的,要么是假的,但不能同时既真又假,也不能模棱两可无法判断其真假.当一个命题改写成“若 p,则 q”的形式之后,判断这种命题的真假的办法是:① 若由“p”经过逻辑推理得出“q”,则可确定“若 p,则 q”是真;确定“若 p,则q”为假,则只需举一个反例说明.② 从集合的观点看,我们建立集合 A,B 与命题中的 p,q 之间的一种特殊联系:设集合 A={x|p(x)成立},B={x|q(x)成立},就是说,A 是全体能使条件 p 成立的对象 x 所构成的集合,B 是全体能使条件 q 成立的对象 x 所构成的集合,此时,命题“若 p,则 q”为真(意思就是“使 p 成立的对象也使 q 成立”),当且仅当 A⊆B 时满足.(3)命题的否定:若 p 表示命题,则“非 p”表示命题的否定.如果命题是“若 p,则q”,那么该命题的否定是“若 p,则綈 q”,即只否定结论.6.全称量词、存在量词与全称量词命题、存在量词命题(1)要判定全称量词命题是真命题,需对集合 M 中每个元素 x,证明 p(x)成立;如果在...