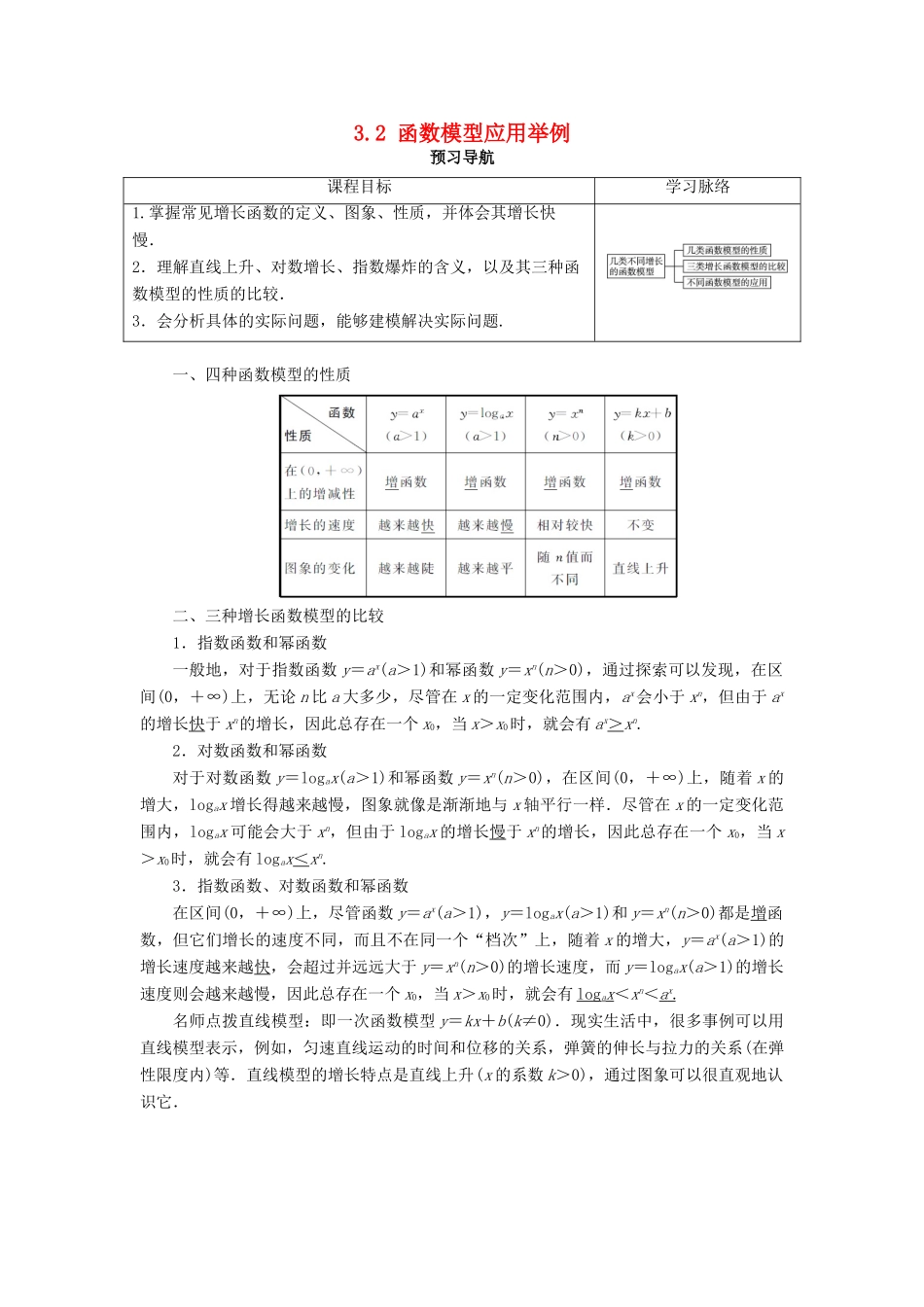
3.2 函数模型应用举例预习导航课程目标学习脉络1.掌握常见增长函数的定义、图象、性质,并体会其增长快慢.2.理解直线上升、对数增长、指数爆炸的含义,以及其三种函数模型的性质的比较.3.会分析具体的实际问题,能够建模解决实际问题.一、四种函数模型的性质二、三种增长函数模型的比较1.指数函数和幂函数一般地,对于指数函数 y=ax(a>1)和幂函数 y=xn(n>0),通过探索可以发现,在区间(0,+∞)上,无论 n 比 a 大多少,尽管在 x 的一定变化范围内,ax会小于 xn,但由于 ax的增长快于 xn的增长,因此总存在一个 x0,当 x>x0时,就会有 ax>xn.2.对数函数和幂函数对于对数函数 y=logax(a>1)和幂函数 y=xn(n>0),在区间(0,+∞)上,随着 x 的增大,logax 增长得越来越慢,图象就像是渐渐地与 x 轴平行一样.尽管在 x 的一定变化范围内,logax 可能会大于 xn,但由于 logax 的增长慢于 xn的增长,因此总存在一个 x0,当 x>x0时,就会有 logax<xn.3.指数函数、对数函数和幂函数在区间(0,+∞)上,尽管函数 y=ax(a>1),y=logax(a>1)和 y=xn(n>0)都是增函数,但它们增长的速度不同,而且不在同一个“档次”上,随着 x 的增大,y=ax(a>1)的增长速度越来越快,会超过并远远大于 y=xn(n>0)的增长速度,而 y=logax(a>1)的增长速度则会越来越慢,因此总存在一个 x0,当 x>x0时,就会有 logax<xn<a x .名师点拨直线模型:即一次函数模型 y=kx+b(k≠0).现实生活中,很多事例可以用直线模型表示,例如,匀速直线运动的时间和位移的关系,弹簧的伸长与拉力的关系(在弹性限度内)等.直线模型的增长特点是直线上升(x 的系数 k>0),通过图象可以很直观地认识它.