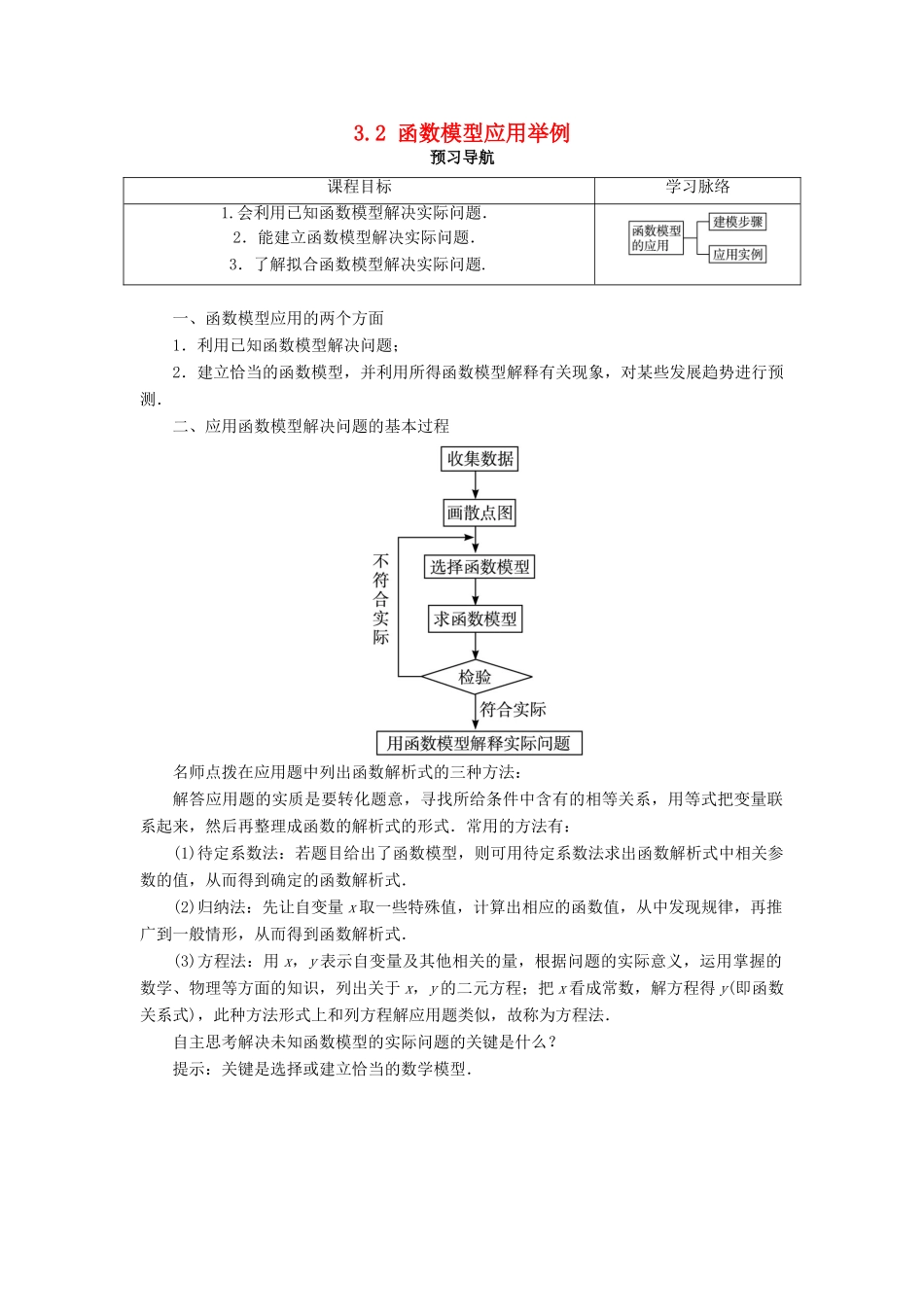
3.2 函数模型应用举例预习导航课程目标学习脉络1.会利用已知函数模型解决实际问题.2.能建立函数模型解决实际问题.3.了解拟合函数模型解决实际问题.一、函数模型应用的两个方面1.利用已知函数模型解决问题;2.建立恰当的函数模型,并利用所得函数模型解释有关现象,对某些发展趋势进行预测.二、应用函数模型解决问题的基本过程名师点拨在应用题中列出函数解析式的三种方法:解答应用题的实质是要转化题意,寻找所给条件中含有的相等关系,用等式把变量联系起来,然后再整理成函数的解析式的形式.常用的方法有:(1)待定系数法:若题目给出了函数模型,则可用待定系数法求出函数解析式中相关参数的值,从而得到确定的函数解析式.(2)归纳法:先让自变量 x 取一些特殊值,计算出相应的函数值,从中发现规律,再推广到一般情形,从而得到函数解析式.(3)方程法:用 x,y 表示自变量及其他相关的量,根据问题的实际意义,运用掌握的数学、物理等方面的知识,列出关于 x,y 的二元方程;把 x 看成常数,解方程得 y(即函数关系式),此种方法形式上和列方程解应用题类似,故称为方程法.自主思考解决未知函数模型的实际问题的关键是什么?提示:关键是选择或建立恰当的数学模型.