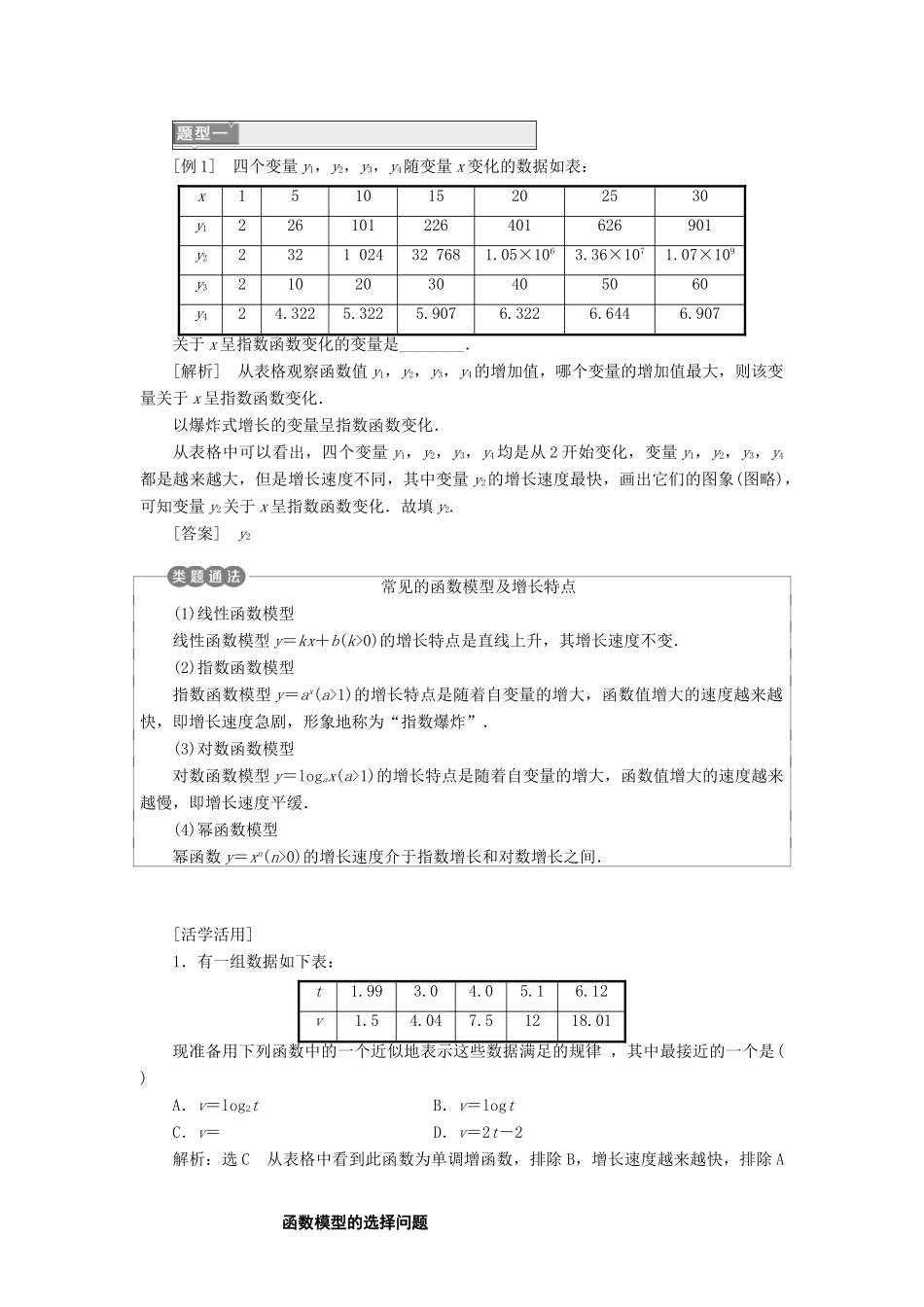
3.2 3.2.1 几类不同增长的函数模型预习课本 P95~101,思考并完成以下问题(1)函数 y=ax(a>1),y=logax(a>1)和 y=xn(n>0)在(0,+∞)上的单调性是怎样的?图象的变化规律是什么? (2)函数 y=ax(a>1),y=logax(a>1)和 y=xn(n>0)的增长速度有什么不同? 指数函数、对数函数和幂函数的增长差异一般地,在区间(0,+∞)上,尽管函数 y=ax(a>1),y=logax(a>1)和 y=xn(n>0)都是增函数,但它们的增长速度不同,而且不在同一个“档次”上.随着 x 的增大,y=ax(a>1)的增长速度越来越快,会超过并远远大于 y=xn(n>0)的增长速度,而 y=logax(a>1)的增长速度则会越来越慢.因此,总会存在一个 x0,使得当 x>x0时,就有 logax < x n < a x ( a >1 , n >0) . 1.判断(正确的打“√”,错误的打“×”)(1)函数 y=x2比 y=2x增长的速度更快些.( )(2)当 a>1,n>0 时,在区间(0,+∞)上,对任意的 x,总有 logax<xn<ax成立.( )答案:(1)× (2)×2.下列函数中随 x 的增大而增大且速度最快的是( )A.y=ex B.y=ln xC.y=x2 D.y=e-x答案:A3.某种产品每件 80 元,每天可售出 30 件,如果每件定价 120 元,则每天可售出 20件,如果售出件数是定价的一次函数,则这个函数解析式为_________________________.答案:y=-x+50(0<x<200)几类函数模型增长差异的比较[例 1] 四个变量 y1,y2,y3,y4随变量 x 变化的数据如表:x151015202530y1226101226401626901y22321 02432 7681.05×1063.36×1071.07×109y32102030405060y424.3225.3225.9076.3226.6446.907关于 x 呈指数函数变化的变量是________.[解析] 从表格观察函数值 y1,y2,y3,y4的增加值,哪个变量的增加值最大,则该变量关于 x 呈指数函数变化.以爆炸式增长的变量呈指数函数变化.从表格中可以看出,四个变量 y1,y2,y3,y4均是从 2 开始变化,变量 y1,y2,y3,y4都是越来越大,但是增长速度不同,其中变量 y2的增长速度最快,画出它们的图象(图略),可知变量 y2关于 x 呈指数函数变化.故填 y2.[答案] y2常见的函数模型及增长特点(1)线性函数模型线性函数模型 y=kx+b(k>0)的增长特点是直线上升,其增长速度不变.(2)指数函数模型指数函数模型 y=ax(a>1)的增长特点是随着自变量的增大,函数值增大的速度越来越快,即增长速度急剧,形象地称为“指数爆炸”.(3)对数函数模型对数...