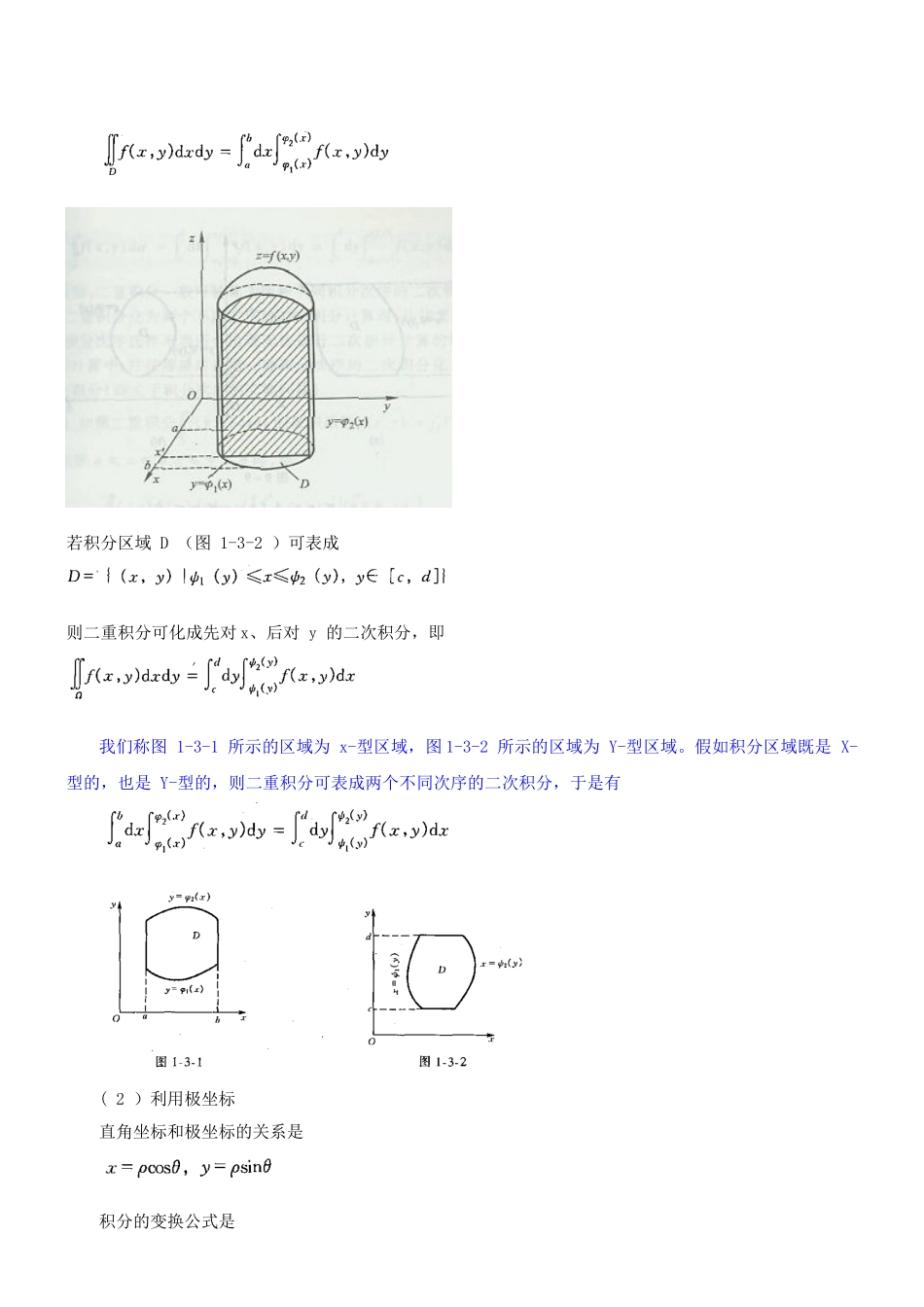
三、重积分(一)重积分的概念与性质 1 .二重积分的概念与性质设 f( x ,y)在平面有界闭区域 D 上有界,将闭区域 D 任意划分成 n 个小闭区域:任取点(i,,) ( i = l , 2 , … ,n)。记小区域的直径为 d i,= max { d 1 , d2 ,…, d n }。若极限总存在,则称此极限为函数 f (x,y )在有界闭区域 D 上的二重积分,记成f( x, y)d,即当 f ( x , y ) 0 , ( x , y ) D 时,二重积分f( x, y)d在几何上表示以曲面Z=f ( x ,y)为顶、闭区域 D 为底的曲顶柱体的体积。二重积分具有如下性质:其中且无内点其中 σ 为 D 的面积( 5 )若在 D 上, f (x,y) ≤ g(x, y),则( 7 )设 M 、m,分别是 f (x,y)在 D 上的最大、最小值, σ 是 D 的面积,则( 8 )设 f (x,y)在闭区域 D 上连续,σ 是 D 的面积,则存在点(ξ , η)∈D,使得2 .三重积分的概念与性质设 f ( x , y ,z)在空间有界闭区域 Ω 上有界,与二重积分的定义类似地有 f(x, y , z )在 Ω上的三重积分的定义,即若 f (x, y , z )表示某物体在点 f ( x , y , z )处的密度,Ω 表示该物体占有的空间闭区域,则三重积分就表示该物体的质量 M . 三重积分具有与二重积分类似的性质。(二)重积分的计算法 1 .二重积分的计算法 ( 1 )利用直角坐标在直角坐标下,二重积分也表成若积分区域 D (图 1-3-1 )可表成则二重积分可化成先对 y 后对 x 的二次积分,即或记成若积分区域 D (图 1-3-2 )可表成则二重积分可化成先对 x、后对 y 的二次积分,即我们称图 1-3-1 所示的区域为 x-型区域,图 1-3-2 所示的区域为 Y-型区域。假如积分区域既是 X-型的,也是 Y-型的,则二重积分可表成两个不同次序的二次积分,于是有( 2 )利用极坐标直角坐标和极坐标的关系是积分的变换公式是若积分区域 D (图 1-3-3 )可表成则二重积分可化成先对 ρ、后对 θ 的二次积分,即2 .三重积分的计算法 ( 1 )利用直角坐标(三)例题1.计算,其中 D 是由抛物线,y2 = x 及直线 y = x - 2 所围成的闭区域。【 解 】 两曲线的交点是( 1,- 1 )、( 4 , 2 )。积分区域 D (图 1-3-4 )可表成从而