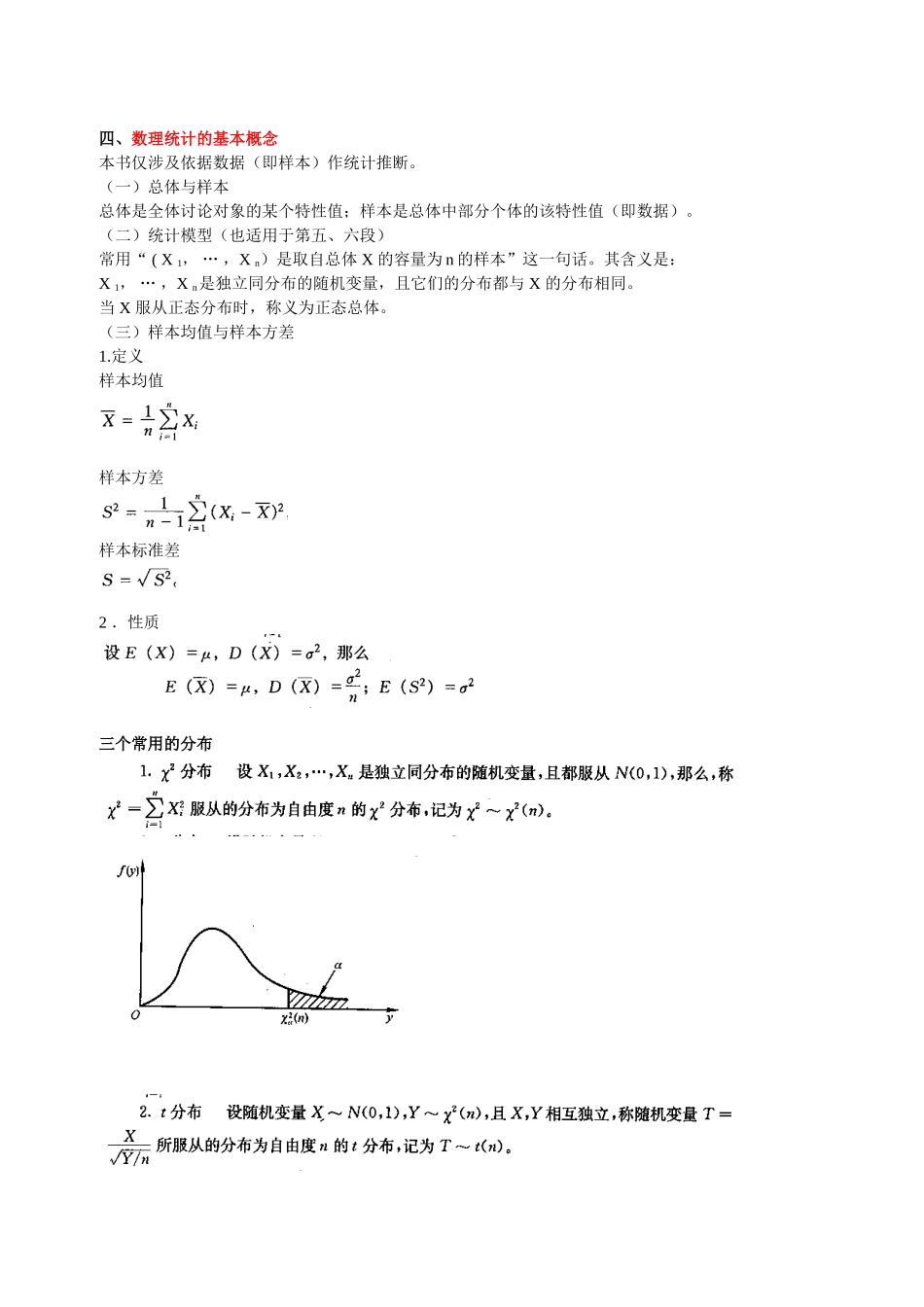
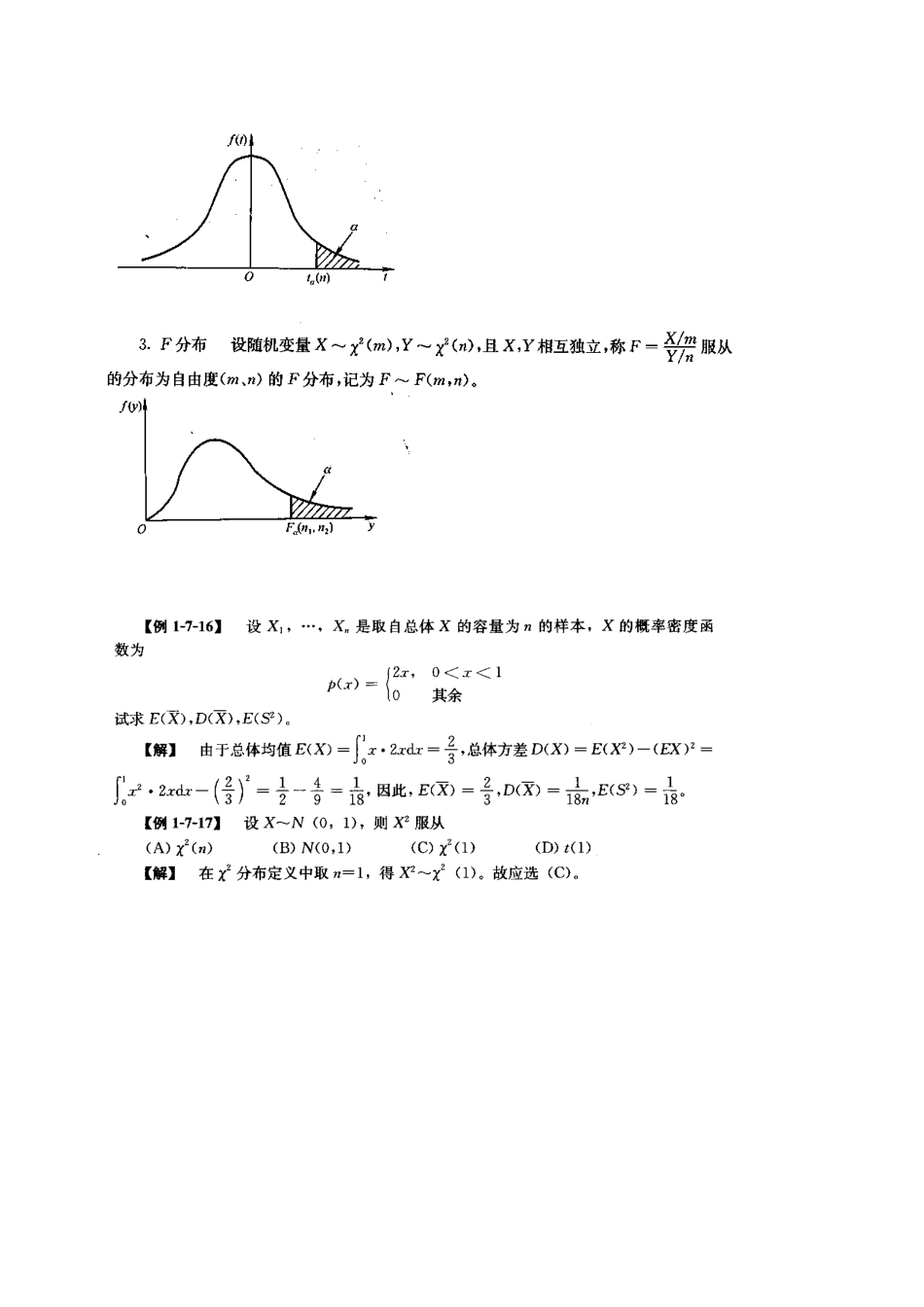
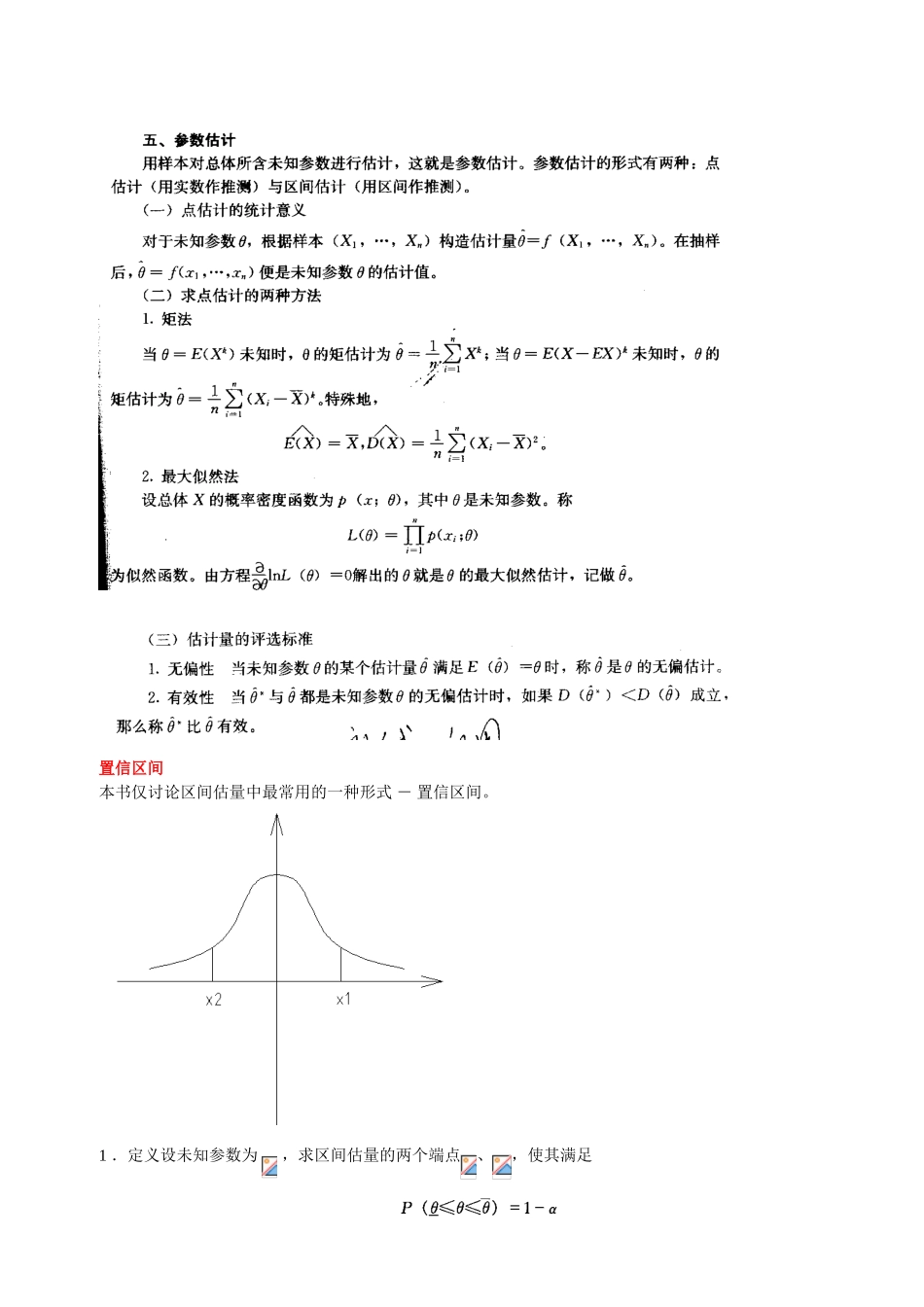
四、数理统计的基本概念本书仅涉及依据数据(即样本)作统计推断。(一)总体与样本总体是全体讨论对象的某个特性值;样本是总体中部分个体的该特性值(即数据)。(二)统计模型(也适用于第五、六段)常用“ ( X 1, … ,X n)是取自总体 X 的容量为 n 的样本”这一句话。其含义是:X 1, … ,X n是独立同分布的随机变量,且它们的分布都与 X 的分布相同。当 X 服从正态分布时,称义为正态总体。(三)样本均值与样本方差1.定义 样本均值样本方差样本标准差2 .性质三个常用的分布置信区间本书仅讨论区间估量中最常用的一种形式 ― 置信区间。1 .定义设未知参数为 ,求区间估量的两个端点、,使其满足其中 l – α 是置信度(或置信水平),常取 90 %、 95 %、 99 %等。称为的置信区间。2 .正态总体中均值的置信区间( 1 )当已知时,在置信度 1 – α 下,的置信区间是,其中 λ 满足.( 2 )当 未知时,在置信度 1-a 下的置信区间是,其中满足 P(= 1 一 a , T 服从自由度为 n- 1 的 t 分布。3 .正态总体 中方差的置信区间设未知。在置信度 1-a 下置信区间是;其中满足 P(x2<) =P(x2>)=, x2服从自由度为 n -1 的 x 2 分布。